Нормированные пространства

Определение. Наименьшая из констант M таких, что , называется нормой оператора А и обозначается .

В частности, выполняется .

Справедливо следующее утверждение: для любого ограниченного

линейного оператора .

§2. Пространства суммируемых функций.

Среди различных классов нормированных пространств, встречающихся в анализе, один из важнейших - это пространство суммируемых функций. Далее будем рассматривать именно эти нормированные пространства.

Определение. Пусть – некоторое фиксированное измеримое множество из . Пространством , где , называется нормированное пространство, элементами которого служат функции , измеримые и почти всюду конечные на , для которых выполняется

Функции, эквивалентные друг другу на , не различаются, а считаются за один и тот же элемент пространства . В частности, нулевой элемент в – это совокупность всех функций, равных нулю почти всюду.

Сложение элементов в и умножение их на числа определяются как обычные сложение и умножение функций. Точнее, поскольку каждый элемент в – это класс эквивалентных между собой функций, то для того, чтобы сложить два таких класса, нужно брать в них по представителю и потом суммой этих классов называют класс, содержащий сумму выбранных представителей. Результат не будет зависеть от выбора представителей в данных классах.

Определение. Число 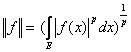называется нормой функции

Будут выполняться все свойства нормы:

1. и почти всюду;

2.

3.

Первое свойство cледует из определения нормы и того, что

Второе – из свойства интеграла: постоянный множитель можно выносить за знак интеграла. Третье свойство вытекает из неравенства Минковского: для любых функций

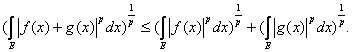
Определение. Функция называется ограниченной почти всюду, если существует неотрицательное число такое, что почти всюду выполняется неравенство . (*)

Определение. Пространством называется нормированное пространство, элементами которого служат почти всюду ограниченные функции . Нормой называется наименьшая из констант, удовлетворяющих неравенству (*).

Для выполняется почти всюду неравенство .

Через будем обозначать линейное пространство измеримых функций, заданных на R.

Среди линейных операторов, действующих в пространстве , рассмотрим следующие.

Определение. Оператор , действующий из пространства () в , называется оператором слабого типа (p,p), если

, где - мера множества, и оператором типа (p,p), если .

По определению оператор типа является ограниченным, что равносильно его непрерывности.

Предложение 1. Любой оператор типа есть оператор слабого типа .

Доказательство.

Нужно доказать, что .

Воспользуемся неравенством Чебышева: .

Возьмем любое положительное число . По неравенству Чебышева

. Но по условию .

Учитывая последнее соотношение, имеем , что и требовалось доказать.

§3. Интеграл Лебега – Стилтьеса.

Далее понадобится понятие интеграла Лебега – Стилтьеса. Введем это понятие.

Определение. Пусть на Rзадана монотонно неубывающая функция , которую для определенности будем считать непрерывной слева. Определим меры всех сегментов, интервалов и полусегментов равенствами

 Скачать реферат