Производные и дифференциалы высших порядков
Задание 1
Вычислить пределы функций:
а). ![]() , б).
, б). 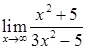 , в).
, в). ![]() , г).
, г). 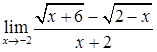 .
.
Решение
а). Для раскрытия неопределенности
разложим знаменатель на множители и сократим дробь.
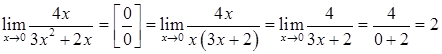 .
.
б). Для раскрытия неопределенности разделим числитель и знаменатель дроби почленно на ![]()
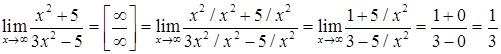 .
.
в). Для раскрытия неопределенности используем следствие из первого замечательного предела ![]() .
.
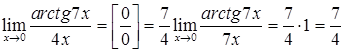 .
.
г). Для раскрытия неопределенность умножим числитель и знаменатель дроби на выражение, сопряженное с числителей и сократим дробь.
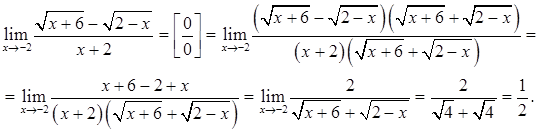
Задание 2
Найти производные заданных функций
а). ![]() ; б).
; б). ![]() ; в).
; в). ![]() .
.
Решение
а). Используем правила дифференцирования суммы функций и сложной функции.
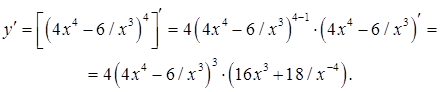
б). Находим производную сложной функции.
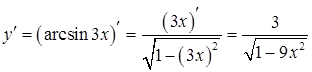 .
.
в). Находим производную сложной функции.
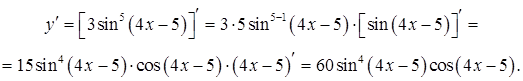
Задание 3
Исследуйте функция и постройте ее график.
![]() .
.
Решение
1. Найдем область определения функции:
![]()
2. Проверим, является ли функция четной или нечетной:
![]() ,
,
следовательно, функция не является ни четной, ни нечетной.
3. Найдем точки пересечения графика функции с осями координат.
С осьюОх: ![]() , тогда
, тогда ![]() .
.
С осью Оу: ![]() , тогда
, тогда ![]() .
.
4. Находим первую производную:
![]()
![]() при
при ![]() .
.
Исследуем знаки производной при переходе через критические точки.
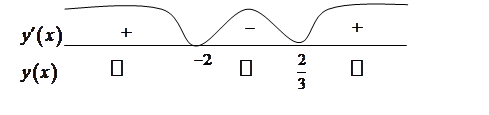
Функция возрастает при . Функция убывает при
. Функция убывает при  .
.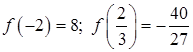 . Получаем
. Получаем ![]() - точка максимума,
- точка максимума, 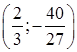 - точка минимума.
- точка минимума.
5. Для нахождения интервалов выпуклости и вогнутости и точек перегиба найдем вторую производную:
![]()
Вторая производная равна нулю при![]() .
.
Наносим на числовую прямую точку ![]() и исследуем знак второй производной на каждом из интервалов.
и исследуем знак второй производной на каждом из интервалов.
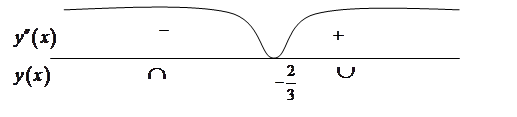
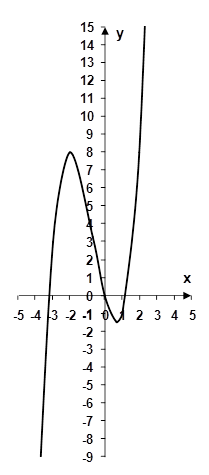
Рис. 1.
В интервале 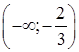 график функции – выпуклый, в интервале
график функции – выпуклый, в интервале 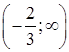 - вогнутый.
- вогнутый. 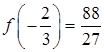 . Получаем
. Получаем  - точка перегиба.
- точка перегиба.
6. Находим асимптоты.
Область определения функции – вся числовая прямая, поэтому вертикальных асимптот нет.
Наклонную асимптоту ищем в виде: ![]() .
.
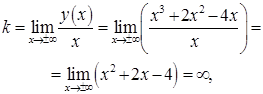
Следовательно, наклонных асимптот нет.
7. Строим график функции (рис. 1):
Задание 4
Найти неопределенные интегралы.
а). ![]() ; б).
; б). ![]() .
.
Решение
а). Используем способ замены переменной.
![]() .
.
б). Используем способ интегрирования по частям.
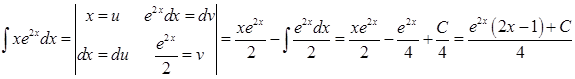
Задание 5
Вычислите площадь фигуры, ограниченной линиями, используя определенный интеграл. Сделайте чертеж.
![]() ,
, ![]() .
.
Решение
Имеем параболу ![]() и прямую
и прямую ![]() . Нужно найти площадь выделенной на рисунке 2 фигуры.
. Нужно найти площадь выделенной на рисунке 2 фигуры.
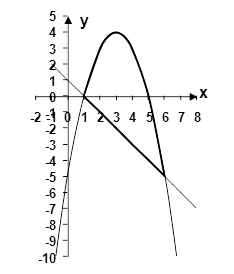
Рис. 2.
Найдем пределы интегрирования (точки пересечения графиков функций), решив систему уравнений:
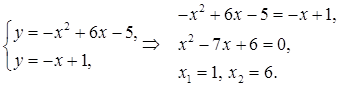
Площадь фигуры равна:
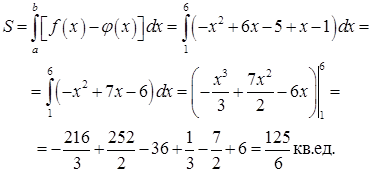
Задание 6
Вычислите по формуле прямоугольников при ![]() определенный интеграл, определите погрешность вычислений:
определенный интеграл, определите погрешность вычислений: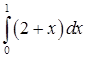 .
.
Решение
функция неопределенный интеграл решение
Формула средних прямоугольников имеет вид:
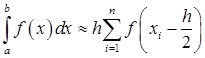 , где
, где ![]() .
.
Согласно условию, ![]() , следовательно,
, следовательно, ![]() .
.
Искомый интеграл равен:
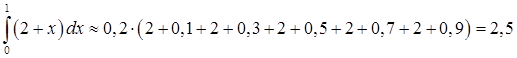 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
