Функция многих переменных

План.

1. Определение функции многих переменных.

2. Предел функции многих переменных. Непрерывность функции многих переменных.

3. Частные производные.

1. Обозначим через D некоторое множество точек в п-мерном пространстве.

Если задан закон f , в силу которого каждой точке М(х; .;х)D ставится в соответствие число и, то говорят, что на множестве D определена функция и= f(х; .;х).

Множество точек М(х; .;х), для которых функция и= f(х; .;х) определена, называют областью определения этой функции и обозначают D(f).

Функции многих переменных можно обозначать одним символом и=f(М), указывая размерность пространства, которому принадлежит точка М.

Функции двух переменных можно изобразить графически в виде некоторой поверхности.

Графиком функции двух переменных z=f(х;у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х;у;z) удовлетворяют уравнению z=f(х;у).

2. Обозначим через (М;М) расстояние между точками М и М. Если п=2, М(х;у), М(х;у), то

(М;М)=.

В п-мерном пространстве

(М;М)=.

Пусть на множестве D задано функцию и=f(М).

Число А называется пределом функции и=f(М) в точке М, если для произвольного числа >0 найдётся такое число >0, что для всех точек МD, которые удовлетворяют условию 0<(М;М)<, выполняется неравенство

.

Свойства пределов функций одной переменной сохраняются и для функций многих переменных, то есть если функции f(М) и g(М) имеют в точке Мконечные пределы, то

1. = с,

2. =,

3. =.

4. 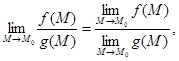если .

Заметим, что если предел существует, то он не должен зависеть от пути, по которому точка М стремится к точке М.

Функция и=f(М) называется непрерывной в точке М, если

= f(М).

Функция и=f(М) называется непрерывной на множестве D, если она непрерывна в каждой точке МD.

Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д. Например, функция z=имеет разрыв в точке (0;0), а функция z=имеет разрыв на параболе

3. Множество точек М, которые удовлетворяют неравенству (М;М)<, называют -окрестностью точки М.

Пусть функция двух переменных z=f(x;у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М (x;у). Дадим переменной х приращение так, чтобы точка (х+;у) принадлежала этой окрестности. При этом функция z=f(x;у) изменится на величину

,

которая называется частичным приращением функции z=f(x;у) по переменной х.

Аналогично величину

называют частичным приращением функции по переменной у.

Если существует предел

,

то его называют частной производной функции z=f(x;у) в точке М (x;у) по переменной х и обозначают такими символами:

 Скачать реферат