Нормированные пространства

Рефераты / Математика / Нормированные пространства

Предложение 4. Множество простых функций всюду плотно в , т.е. , такая, что >,где – простая функция.

Доказательство.

I.Обозначим 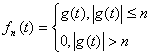, где N.

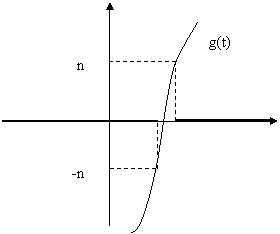Ясно, что для почти всех . Тогда для почти всех . Следовательно, .

С другой стороны, (*) ,т.е. . Поэтому суммируема. Применим теорему Лебега к неравенству (*) :. Получим, что и, значит, приблизили функциями . Возьмем произвольное положительное число . Найдем функцию такую, что .

II. Приблизим ступенчатой функцией.

Обозначим , где . Положим .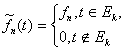

По свойству интеграла Лебега для любого положительного найдется , такое, что . Это означает, что .

Отрезок разобьем на равных частей точками так, чтобы .

Обозначим

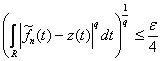Рассмотрим функцию . Тогда . Следовательно, , т.е. .

В результате нашлась простая функция такая, что

III. Таким образом, . Предложение доказано.

Первая интерполяционная теорема в теории операторов была получена М.Риссом в 1926 году в виде некоторого неравенства для билинейных форм. Ее уточнение и операторная формулировка были даны Г.О.Ториным. Вся теория интерполяции линейных операторов первоначально развивалась в направлении обобщения этой теоремы. Дадим ее формулировку.

Теорема. Пусть . Оператор Т действует из пространства в с нормой и одновременно из в с нормой .Тогда Т будет непрерывным оператором из пространства в с нормой , удовлетворяющей неравенству при условии, что 0<t<1 и ; .

Теперь рассмотрим приложение теоремы Рисса – Торина в доказательстве следующего факта.

Теорема. Пусть и для чисел выполняется равенство .Тогда свертка .

Доказательство.

Нужно доказать, что , т.е. 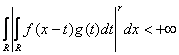. Зафиксируем произвольную функцию из . Докажем сначала требуемый результат для частного случая, когда функция g простая, а затем распространим на произвольные функции g.

I. Пусть функция простая.

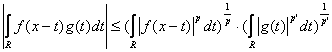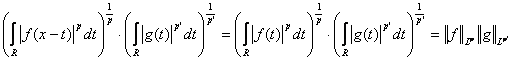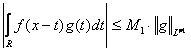1) Рассмотрим оператор свертки на множестве простых функций и проверим, что он типа , где . В силу неравенства Гельдера . Учитывая геометрический смысл интеграла, получим для любого действительного числа х. Тогда . Так как , то , т.е. равна некоторому числу . Таким образом, . Следовательно, нашлась константа , такая, что . Это и означает, что оператор свертки Т на множестве простых функций типа .