Связь комбинаторики с различными разделами математики

Содержание

Введение . 3

§1. Применение леммы Бернсайда к решению комбинаторных задач . 5

1.1. Орбиты группы перестановок 5

1.2. Длина орбиты группы перестановок. Лемма Бернсайда 5

1.3. Комбинаторные задачи 8

§2. «Метод просеивания» 21

2.1. Формула включения и исключения 21

2.2. Общий «метод просеивания» или «пропускания через решето». Реше

то Сильва-Сильвестра . 23

2.3. Использование общего метода решета в теории чисел . 23

§3. Разбиение фигур на части меньшего диаметра 28

§4. «Счастливые билеты» 34

Библиографический список . 39

Введение

Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов называется комбинаторикой. Комбинаторика возникла в XVI веке. Вопросы, касающиеся азартных игр, явились движущей силой в развитии комбинаторики. Сейчас комбинаторные методы применяются как в самой математике, так и вне её – теория кодирования, планирование эксперимента, топология, конечная алгебра, математическая логика, теория игр, кристаллография, биология, статистическая физика, экономика и т.д.

Комбинаторика, пройдя многовековой путь развития, обретя собственные методы исследования, с одной стороны, широко используется при решении задач алгебры, геометрии, анализа, с другой стороны, сама использует геометрические, аналитические и алгебраические методы исследования.

Цель дипломной работы: показать связь комбинаторики с различными разделами математики.

Задачи:

1. Изучить лемму Бернсайда и решить комбинаторные задачи о раскраске с её применением;

2. Показать применение метода «просеивания» для подсчёта количества простых и взаимно простых чисел;

3. Рассмотреть теорему Борсука, которая решает задачу для плоских фигур о разбиении их на части меньшего диаметра;

4. Решить задачу о «счастливых билетах».

Дипломная работа состоит из четырёх частей:

В § 1 рассмотрена связь теории групп с комбинаторикой: применение группы перестановок к решению комбинаторных задач. Основной используемый факт в этом параграфе – лемма Бернсайда.

В § 2 показан наиболее общий метод пересчёта (известный ещё в XVIII веке), а также приведены примеры его использования в теории чисел.

Параграф 3 посвящён вопросу комбинаторной геометрии – вопросу о разбиении фигуры на несколько меньших частей. Рассмотренная теорема Борсука является тем стержнем, вокруг которого возможно дальнейшее рассмотрение этого вопроса.

В § 4 решается известная задача о счастливых билетах с привлечением методов из математического анализа.

§ 1. Применение леммы Бернсайда к решению комбинаторных задач [3]

1.1. Орбиты группы перестановок

Пусть G – группа перестановок на множестве М={1, 2, …, n}. Подмножество ОМ называется орбитойгруппы G, если: а) α(a)O для любого αG и любого aO, то есть действие перестановок из G на элементы О не выводит за пределы О; б) любые два элемента из О можно перевести друг в друга некоторой перестановкой из G.

Легко показать, что всякая группа перестановок G={ε=α0, α1, …, αk-1} имеет орбиты.

Орбитами подобного вида исчерпываются все типы орбит, то есть, если О – орбита группы G и аО, то О=О(а).

Любые две орбиты О(а) и О(b) либо совпадают (если bO(a)), либо не пересекаются (если bO(a)).

Таким образом, множество М распадается в объединение непересекающихся подмножеств – орбит группы G. В связи с разбиением множества М на орбиты группы перестановок G возникают следующие два вопроса:

1) Сколько орбит имеет группа G на множестве М?

2) Какова длина каждой из этих орбит, то есть из скольких элементов они состоят?

Ответим на эти вопросы.

1.2. Длина орбиты группы перестановок. Лемма Бернсайда

Ответим на второй вопрос. Для любого элемента аМ можно рассмотреть группу Ga всех перестановок из G, для которых точка а является неподвижной. Она называется стабилизатором точки а. Ответим на вопрос, доказав следующую теорему:

Длина орбиты О(а) равна индексу стабилизатора Ga в группе G, то есть |O(a)|= | G |:| Ga |.

Доказательство. Пусть G={ε=α0, α1, …, αk-1}, Ga={ε=β0, β1, …, βs-1}. Для подсчёта различных элементов в последовательности a=α0(a), α1(a), …, αk-1(a) удобно особым образом расположить в ряд элементы группы G. Для этого используем тот факт, что группу G можно представить в виде объединения всевозможных непересекающихся правых классов смежности по подгруппе Ga, имеющих одинаковое число элементов. То есть существуют перестановки γ0=ε, γ1, …, γl-1 из группы G такие, что все перестановки ряда

α0= β0° γ0= ε, α1= β1° γ0, …, αs-1= βs-1° γ0,

αs= β0° γ1, αs+1= β1° γ1, …, α2s-1= βs-1° γ1, (*)

- - - - - - - - - - - - - - - - - - - - - - - - - - - -

α(l-1)s= β0° γl-1, α(l-1)s+1= β1° γl-1, …, αls-1= βs-1° γl-1

попарно различны и исчерпывают всю группу G.

Для любого i=0, …, l-1 применение s перестановок αis, αis+1, …, α(i+1)s-1, образующих i-тую строку таблицы (*), к элементу а даёт один и тот же элемент γi(а) (так как β0, β1, …, βs-1 оставляют а неподвижным). Все l элементов γi(а) попарно различны. Действительно, если бы γi(а)=γj(а) для некоторых i, j, то а=(γj ° γi-1) (a), то есть перестановка (γj ° γi-1)Ga. Но это возможно только тогда, когда γi и γj содержатся в одном правом классе смежности группы G по подгруппе Ga, чего быть не может. Таким образом, длина орбиты О(а) равна l, то есть числу строк в таблице (*): k=l∙s (то есть l является индексом подгруппы в группе). По теореме Лагранжа l=| G |:| Ga |, то есть |O(a)|= | G |:| Ga |. Теорема доказана.

Теперь ответим на первый вопрос. Для этого сформулируем и докажем лемму Бернсайда.

Пусть λ(α) – число неподвижных точек перестановки α, t(G) – число орбит группы перестановок G={ε=α0, α1, …, αk-1}, действующей на множестве М={1, 2, …, n}. Тогда для любой группы перестановок имеет место равенство:

t(G)=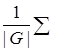λ(α), где αG.

 Скачать реферат