Дифференциальные уравнения с запаздывающим аргументом

1. Определения

Дифференциальные уравнения с запаздывающим аргументом вида

(1)

где , , , называются диф

ференциальными уравнениями с запаздыванием, зависящим от состояния, а именно с сосредоточенным запаздыванием.

Если заданы начальные данные в виде

(2)

То имеет смысл определить понятие решения, начинающегося в точке σ с функции φ, или, короче, начинающегося в φ.

В дальнейшем будем рассматривать только решения, удовлетворяющие условию Липшица, поэтому следует дать следующее определение:

Def 1.Функция называется решением системы (1), (2) на отрезке , если она удовлетворяет следующим условиям:

на отрезке .

Естественно возникает вопрос о существовании и единственности такого решения.

Для начала сделаем некоторые обозначения.

a) есть функция, определенная на отрезке и удовлетворяющая условию Липшица с константой L, то есть

;

b)

c)

Def 2.удовлетворяет условиям a),b),c)}

2. Полезная лемма

Lemma 1: -выпуклое, замкнутое, ограниченное множество в пространстве непрерывных на отрезке функций.

Proof:

1)Выпуклость:

a)Выберем произвольные функции , тогда

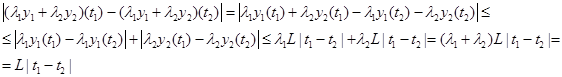
b);

c)на отрезке на том же отрезке для любых .

2)Ограниченность:

Множество определено так, что все элементы этого множества лежат в шаре радиуса

3)Замкнутость:

Возьмем последовательность функций такую, что

, .

a)

Возьмем тогда

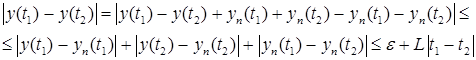
Так как это верно при любом , то получаем, что предельная функция удовлетворяет условию Липшица с константой L.

b) По теореме Кантора равномерно на отрезке.

Предположим, что при этом (для простоты доказательства предположим что , если , рассуждения проводятся аналогично)

Возьмем 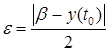, тогда, так как для любого положительного и любого выполнено , то выполнено и для данных и t. Получим:

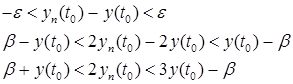
Так как по предположению , то получаем что , а это невозможно, так как . Противоречие показывает, что предельная функция ограничена по норме той же константой .

c)

на отрезке .

Видим, что выполнение условий a,b,c равнозначно тому что , то есть множество замкнуто.

Лемма доказана полностью.

3. Существование и единственность решения

Для доказательства теоремы о существовании и единственности липшицевого решения нам потребуется некоторые понятия и важные теоремы, доказательства которых можно, например, найти в книге Кадеца [3].

Def 2. Оператор Т называется вполне непрерывным (компактным), если Т непрерывен и Т отображает любое ограниченное множество в предкомпактное.

Def 3. Семейство Ф функций φ, определенных на называется равномерно ограниченным, если

Def 4.Семейство Ф функций φ, определенных на , называется равностепенно непрерывным, если

Теорема 1.(Арцела)

Для того чтобы семейство Ф непрерывных, определенных на отрезке функций было предкомпактом в , необходимо и достаточно, чтобы это семейство было равномерно ограниченным и равностепенно непрерывным.

 Скачать реферат