Гипергеометрическое уравнение
u=A F(![]() ,
, ![]() ,
, ![]() ,z)+B
,z)+B![]() F(1-
F(1-![]() +
+![]() ,1-
,1-![]() +
+ ![]() ,2-
,2- ![]() ,z), (2.20)
,z), (2.20)
где А и В произвольные постоянные ![]() <1,
<1, ![]()
2. Представление различных функций через гипергеометрическую
Гипергеометрическая функция F(![]() ,
, ![]() ,
, ![]() ,z) приводится к полиному, когда
,z) приводится к полиному, когда ![]() =0,-1,-2,… или
=0,-1,-2,… или ![]() =0,-1,-2. Например,
=0,-1,-2. Например,
F(![]() , 0,
, 0, ![]() ,z)=
,z)= ![]()
![]() zk=
zk=![]() =1,
=1,
так как
![]() =0(0+1)(0+2)… (0+k-1)=0.
=0(0+1)(0+2)… (0+k-1)=0.
F(![]() , -2,
, -2, ![]() ,z)=
,z)= ![]()
![]() zk=
zk=![]() z0+
z0+![]() z+
z+![]() z2 =
z2 =
=1-2![]() z+
z+![]() z2,
z2,
так как
![]() =1,
=1, ![]() =-2,
=-2,
![]() =(-2)(-1)=2,
=(-2)(-1)=2, ![]() =(-2)(-1)0=0,
=(-2)(-1)0=0, ![]() =(-2)(-1)01=0
=(-2)(-1)01=0
и так далее.
Преобразование
F(![]() ,
, ![]() ,
, ![]() ,z)=(1-z
,z)=(1-z![]() F(
F(![]() -
-![]() ,
,![]() -
-![]() ,
, ![]() ,z)
,z)
![]() -
-![]() =0
=0![]()
![]() =
=![]()
показывает, что гипергеометрическая функция при ![]() -
-![]() =0,-1,-2,… или
=0,-1,-2,… или ![]() -
-![]() =0,-1,-2,… выражается через алгебраические функции. В частности,
=0,-1,-2,… выражается через алгебраические функции. В частности,
F(![]() ,
, ![]() ,
, ![]() ,z)= (1-z
,z)= (1-z![]() ,
, ![]() (3.1)
(3.1)
Придавая параметрам ![]() ,
, ![]() специальные значения, находим
специальные значения, находим
(1-z)v= F(-v, 1, 1,z)
(1-z![]() = F(
= F(![]() , 1, 1,z) (3.2)
, 1, 1,z) (3.2)
(1-z)n= F(-n, ![]() ,
, ![]() ,z)
,z)
n=0,1,2,…
Чтобы получить представление логарифмической функции, воспользуемся разложением
ln(1-z)= - ![]()
![]() =-z
=-z![]()
![]()
![]() <1
<1
откуда следует
ln(1-z)=-zF(1,1,2,z) ![]() . (3.3)
. (3.3)
Аналогичным образом выводятся формулы для обратных круговых функций:
arctg z=zF(![]() ,1,
,1, ![]() ,-z2)
,-z2) ![]() (3.4)
(3.4)
arcsin z=zF(![]() ,
,![]() ,
, ![]() ,z2)
,z2) ![]()
arctg z=![]() (-1)k
(-1)k![]() =z
=z![]()
![]() =z
=z![]()
![]() =
=
=z![]()
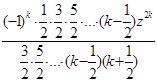 =z
=z ![]()
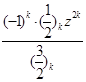 =z
=z![]()
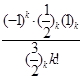 =zF(
=zF(![]() ,1,
,1, ![]() ,-
,-
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
