Объем фигур вращения правильных многогранников

Содержание

Введение. Фигуры вращения правильных многогранников

1. Виды поверхностей в фигурах вращения

2. Теорема о пересечении гиперболической и цилиндрической поверхностей вращения

3. Классификация задач на вращение многогранников

4. Решение задач на вращение многогранников

Заключение

Список литературы

Введение

Каждое геометрическое тело име

ет поверхность, и если она состоит из плоских многоугольников, то такое тело называется многогранником, а составляющие его поверхность многоугольники – гранями. Границы между гранями называются ребрами, а точки, в которых ребра соединяются, — вершинами многогранника.

Таким образом, многогранники – это тела, ограниченные плоскими многоугольниками. Они окружают нас повсюду: ведь самая популярная форма современного здания, телевизора, мебели – параллелепипед. Например, рассмотрим

o Использование теории правильных многогранников в архитектуре

o Национальная библиотека в Минске (Авторы проекта здания – Михаил Виноградов и Виктор Крамаренко.)

o Перевернутая пирамида – использованная при построении здании современного искусства в Каракасе (Архитектор Оскар Нимейер).

o Звездчатые многогранники – создание на их основе проектов административного здания в Италии и национальной библиотеки в Дамаске (В.А. Сомов, А.М. Бреславец, В.Н. Гамаюнов).

Объектом исследования в данной исследовательской работе являются фигуры вращения правильных многогранников. Предмет исследования – объем тел вращения.

Работая над темой, мне удалось собрать удивительно интересный материал о правильных многогранниках. Оказалось, что даже тайна мироздания связана с этими пятью правильными многогранниками.

В процессе исследования были построены развертки и модели многогранников, сформулированы и решены задачи на вычисление объемов фигур вращения.

Фигуры вращения правильных многогранников

Поверхностью вращения называют фигуру, которая получается вращением какой-либо линии.

Если для какой-то фигуры существует прямая, любой поворот вокруг которой совмещает фигуру саму с собой, то эту фигуру называют фигурой вращения. При этом прямая, любой поворот вокруг которой отображает фигуру саму на себя, называется осью вращения.

Телом вращения называют всякое геометрическое тело, которое является фигурой вращения.

Тела вращения характеризуются линией, которая при своем вращении относительно оси образует поверхность тела вращения. Эту линию для данного тела вращения называю образующей.

1. Виды поверхностей в фигурах вращения

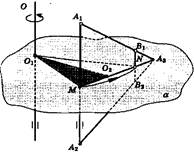
Образующими поверхностей вращения в задачах представленных в данной работе служат ребра многогранника, т.е. общие стороны двух граней многогранника.

При вращении любого многогранника вокруг произвольной оси получается тело вращения, которое может быть ограничено только следующими поверхностями:

o плоскостью;

o цилиндрической поверхностью;

o конической поверхностью;

o поверхностью однополостного гиперболоида.

Если прямая (образующая поверхности) перпендикулярна оси вращения, то получается плоскость.

Если прямая (образующая поверхности) параллельна оси вращения, то получается цилиндрическая поверхность.

Если прямая (образующая поверхности) пересекает ось вращения, то получается коническая поверхность.

Если прямая (образующая поверхности) скрещивается с осью вращения, то получается однополостный гиперболоид вращения.

Итак, если прямая (образующая поверхности) скрещивается с осью вращения, то получается однополостный гиперболоид вращения.

Образующими поверхности однополостного гиперболоида в рассматриваемых задачах являются ребра многогранников, лежащие на прямых, скрещивающихся с осью вращения.

2. Теорема о пересечении гиперболической и цилиндрической поверхностей вращения

Правильные многогранники можно вписать в сферу, поэтому все задачи на вращение правильных многогранников, содержащие пересекающиеся поверхности вращения, удовлетворяют следующей теореме.

Теорема Монжа

Две поверхности второго порядка, которые касаются третьей поверхности второго порядка по плоским кривым линиям, пересекаются между собой по плоским кривым линиям второго порядка.

Очевидно, что в рассматриваемых задачах на вращение правильных многогранников линиями пересечения поверхностей вращения являются окружности.

Как отмечалось, фигуры, полученные в результате вращения многогранника относительно произвольной оси, ограничены лишь такими видами поверхностей как:

o коническая поверхность,

o цилиндрическая поверхность,

o круг или кольцо,

o однополостный гиперболоид.

В задачах 3.2 и 4.2 пересекаются поверхность однополостных гиперболоидов с цилиндрической поверхностью. Образующими этих поверхностей вращения являются ребра многогранников, которые, будучи сторонами правильных многоугольников с нечетным числом сторон, несут в себе интересную закономерность относительно высот каждого вида указанных поверхностей для фигуры вращения.

3. Классификация задач на вращение многогранников

Правильный тетраэдр - четырехгранник.

Вычислить объем тела, полученного вращением тетраэдра относительно оси, проходящей через его ребро, если ребро тетраэдра равно a.

Вычислить объем тела, полученного вращением тетраэдра относительно оси, проходящей через центр грани и противоположную вершину, если ребро тетраэдра равно a.

Вычислить объем тела, полученного вращением тетраэдра относительно оси, проходящей через среднюю линию боковой грани, если ребро тетраэдра равно a.

Куб (или правильный гексаэдр)- шестигранник

Вычислить объем тела, полученного вращением куба относительно оси, проходящей через противоположные вершины, если ребро куба равно a.

Вычислить объем тела, полученного вращением куба относительно оси, проходящей через середины его противоположных ребер, если ребро куба равно a.

Вычислить объем тела, полученного вращением куба относительно оси, проходящей через центры его противоположных граней, если ребро куба равно a.

Октаэдр- восьмигранник

Вычислить объем тела, полученного вращением октаэдра относительно оси, проходящей через противоположные вершины, если ребро октаэдра равно a.

Вычислить объем тела, полученного вращением октаэдра относительно оси, проходящей через середины его противоположных ребер, если ребро октаэдра равно a.

 Скачать реферат