Минимизация неполностью определенных переключательных функций

В ЦВМ могут использоваться комбинационные схемы, закон функционирования которых определен неполностью. В таких схемах некоторые комбинации сигналов на ее входы не подаются и являются запрещенными.

Для запрещенных входных комбинаций выходные сигналы не определены, т.е. могут принимать любые значения – нуль или единицу. Поэтому при синтезе схем с неполностью заданным законом функционировани

я можно произвольно задать значения выходных сигналов для запрещенных комбинаций входных сигналов; нормальная работа схемы при этом не нарушается.

Выходным сигналам на запрещенных комбинациях придают такие значения, при которых можно построить наиболее простую схему.

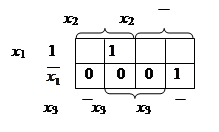
Схемы с запрещенными комбинациями выходных сигналов описываются неполностью определенными переключательными функциями, т.е. функциями, значения которых определены не на всех наборах. Например, функция заданная таблицей и диаграммой Вейча

определена только на шести наборах. Клетки, соответствующие наборам 1,0,0; 1,1,1 остаются пустыми.

Форма представления функции f(x1, x2, x3) существенно зависит от выбора ее значений на запрещенных наборах, Например, для заданной функции, выбирая ее запрещенные значения равными нулю, можно получить минимальную ДНФ в виде

Если значения функции на запрещенных наборах принять равными единице, то форма представления упрощается

.

Рассмотрим общую методику получения минимальных ДНФ неполностью определенных переключательных функций

Определение Пусть переключательная функция f(x1, x2, …, xn) не определена на p наборах аргументов. Тогда полностью определенную функцию j(x1, x2, …, xn) будем называть эквивалентной функции f(x1, x2, …, xn), если ее значения совпадают со значениями функции f(x1, x2, …, xn) на тех наборах, на которых эта функция f определена.

Существует 2p вариантов выбора значений функции на запрещенных наборах и, следовательно, 2р различных переключательных функций, эквивалентных функции f(x1, x2, …, xn).

Поэтому задача минимизации неполностью определенной функции f(x1, x2, …, xn) сводится к отысканию такой эквивалентной функции j(x1, x2, …, xn), которая имеет простейшую минимальную форму.

Введем эквивалентные функции j0(x1, x2, …, xn) и j1(x1, x2, …, xn), значения которых на всех запрещенных наборах функции f(x1, x2, …, xn) равны, соответственно, нулю и единице.

Теорема. Минимальная ДНФ неполностью определенной функции f(x1, x2, …, xn) совпадает с дизъюнкцией самых коротких импликант эквивалентной функции j1(x1, x2, …, xn), которые совместно поглощают все конституенты единицы функции j0(x1, x2, …, xn) и ни одна из которых не является лишней.

Для доказательства теоремы рассмотрим СДНФ некоторой эквива­лент­ной функции ji(x1, x2, …, xn). Конституенты единицы, входящие в эту форму, обязательно войдут и в СДНФ функции j1(x1, x2, …, xn). Поэтому любая простая импликанта функции ji(x1, x2, …, xn) будет совпадать с импликантой функции j1(x1, x2, …, xn) или будет поглощаться ею. Другими словами, среди импликант функции j1(x1, x2, …, xn) всегда найдется такая, которая поглощает любую импликанту любой эквивалентной функции ji(x1, x2, …, xn). Следовательно, самыми короткими произведениями, накрывающими единицы функции f(x1, x2, …, xn), будут импликанты j1(x1, x2, …, xn).

Среди всех ПФ, эквивалентных заданной, функция j0(x1, x2, …, xn) имеет минимальное количество конституент единицы. Следовательно, и количество простых импликант [из набора импликант функции j1(x1, x2, …, xn)], необходимых для поглощения конституент функции j0(x1, x2, …, xn), будет минимальным. Если составить дизъюнкции наиболее коротких импликант функции j0(x1, x2, …, xn), которые совместно накрывают все конституенты единицы функции j0(x1, x2, …, xn), то получим, очевидно, минимальную форму представления функции f(x1, x2, …, xn).

Ввиду того, что для накрытия единиц функции j0(x1, x2, …, xn) выби­раются импликанты другой функции, дизъюнкция этих импликант не равняется функции j0(x1, x2, …, xn). Однако, такая дизъюнкция обязательно равна одной из функций, эквивалентных функции f(x1, x2, …, xn).

Пример. Найти минимальную дизъюнктивную нормальную форму ПФ, заданной таблицей.

 Скачать реферат