Гипергеометрическое уравнение

z2),

так как =1*2*…*k=k!

arcsin z=z+=z[1+]=

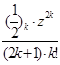=z[1+height=45 src="images/referats/7523/image166.png">]=z[1+]=z[1+] =

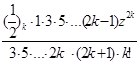=z[1+]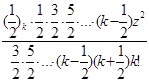=z[1+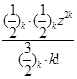= zF(,, ,z2).

3. Вырожденная гипергеометрическая функция

Наряду с гипергеометрической функцией F(,,,z), важную роль в теории специальных функций играет так называемая вырожденная гипергеометрическая функция F(, ,z).

Чтобы определить эту функцию, заметим, что степенной ряд

,

где z – комплексное переменное, и - параметры, которые могут принимать любые вещественные или комплексные значения, исключая =0,-1,-2,… и символ обозначает величину

==1

сходится при любых конечных z.

Так как, если обозначить через общий член ряда, то

=0, когда k.

Вырожденная гипергеометрическая функция F(, ,z) определяется как сумма рассматриваемого ряда

F(, ,z)= , 0,-1,-2,…, <(4.1)

Из данного определения вытекает, что F(, ,z) функция комплексного переменного z.

Если положить

f(, ,z)= F(, ,z)= , (4.2)

то f(, ,z) при фиксированном z будет целой функцией от и . Действительно, члены ряда (6.2) являются целыми функциями этих переменных, и ряд сходится равномерно в области <A, <C.

Полагая , имеем для достаточно больших k

=

Отсюда следует, что при заданном z функция F(, ,z)

представляет целую функцию и мероморфную функцию с простыми полюсами в точках =0,-1,-2,…

Функция F(,,z) весьма часто встречается в анализе, причем главное ее значение состоит в том, что многие специальные функции могут рассматриваться как ее частные случаи, что в значительной мере облегчает построение теории этих функций и придает ей общий и компактный характер.

Связь функции F(,,z) с гипергеометрической функцией дается соотношением

F(,,z)=lim F(,,,). (4.3)

Из определения вырожденной гипергеометрической функции непосредственно вытекают равенства

 Скачать реферат