Гипергеометрическое уравнение
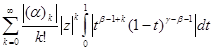
![]()
![]()
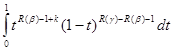
![]() =
=
=![]() F(<
F(<
img width=20 height=27 src="images/referats/7523/image027.png">, R(![]() ),R(
),R(![]() ),
),![]() )
)
На основании известного биноминального разложения
![]() =(1-tz)-a(1.3)
=(1-tz)-a(1.3)
0![]() t
t![]() 1,
1,![]() <1
<1
поэтому для F(![]() ,
, ![]() ,
, ![]() ,z) получается представление
,z) получается представление
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= 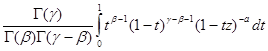 (1.4)
(1.4)
R(![]() )>R(
)>R(![]() ) >0 и
) >0 и ![]() <1
<1
Покажем, что интеграл в правой части последнего равенства сохраняет смысл и представляет регулярную функцию комплексного переменного z в плоскости с разрезом (1, ![]() ).
).
Для z принадлежащих области ![]() ,
, ![]() (R – произвольно большое,
(R – произвольно большое, ![]() и
и ![]() произвольно малые положительные числа), и 0 < t < 1 подынтегральное выражение есть регулярная функция z и непрерывная функция t ; поэтому достаточно показать что интеграл сходится равномерно в рассматриваемой области. Доказательство следует из оценки
произвольно малые положительные числа), и 0 < t < 1 подынтегральное выражение есть регулярная функция z и непрерывная функция t ; поэтому достаточно показать что интеграл сходится равномерно в рассматриваемой области. Доказательство следует из оценки
![]()
(М – верхняя граница модуля функции (1-tz)-a, непрерывной в замкнутой области ![]() ,
, ![]() , 0
, 0![]() t
t ![]() 1), которая показывает, сходимость интеграла будет мажорированной, то есть при R(
1), которая показывает, сходимость интеграла будет мажорированной, то есть при R(![]() )>R(
)>R(![]() ) >0 интеграл
) >0 интеграл 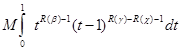 сходится.
сходится.
Таким образом, условие ![]() <1 в (1.4) может быть отброшено, и искомое аналитическое продолжение гипергеометрической функции в разрезанную плоскость дается формулой
<1 в (1.4) может быть отброшено, и искомое аналитическое продолжение гипергеометрической функции в разрезанную плоскость дается формулой
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= 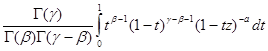 (1.5)
(1.5)
R(![]() )>R(
)>R(![]() ) >0;
) >0; ![]()
В общем случае, когда параметры имеют произвольные значения, аналитическое продолжение F(![]() ,
, ![]() ,
, ![]() ,z) плоскость с размером (1,
,z) плоскость с размером (1, ![]() ) может быть получено в форме контурного интеграла, к которому приводит суммирование ряда (1.1) с помощью теории вычетов.
) может быть получено в форме контурного интеграла, к которому приводит суммирование ряда (1.1) с помощью теории вычетов.
Более элементарный метод продолжения, не дающий, однако, возможность получить в явной форме общее аналитическое выражение гипергеометрической функции, заключается в использовании рекуррентного соотношения (1.6)
![]() F(
F(![]() ,
, ![]() ,
, ![]() ,z) =
,z) = ![]() +
+ ![]()
справедливость которого может быть установлена подстановкой в него ряда (1.1). После подстановки и приведения подобных членов коэффициент при zk в правой части (1.6) будет
![]()
![]() +
+![]() -
- ![]() = =
= =![]() {
{![]()
![]() -
-![]()
![]() -
-![]() }= =
}= =![]() (
(![]()
![]()
![]()
![]()
Путем повторного применения этого тождества можно представить функцию F(![]() ,
, ![]() ,
, ![]() ,z) с произвольными параметрами (
,z) с произвольными параметрами (![]()
![]() 0,-1,-2,…) в виде суммы
0,-1,-2,…) в виде суммы
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)= ![]() F(
F(![]() +s,
+s, ![]() +p,
+p, ![]() +2p, z) (1.7)
+2p, z) (1.7)
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
