Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства

Рис. 7. Рис. 8.

Ясно, что в случае рис. 7 А = (-(, в случае рис. 8 А = .

Включение в первом случае соответствует системе неравенств

<

img width=59 height=40 src="images/referats/642/image322.gif">, во втором случае автоматически.

Из пункта II теоремы 7 вытекают условия:

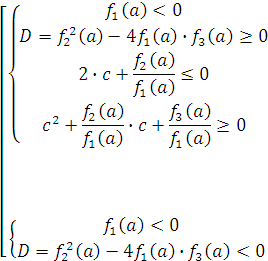
Окончательный ответ задачи получается объединением ответов из пунктов 2а), 2б) и 2в).

Задание: выписать самостоятельно схемы решений следующих задач:

III. Найти все значения параметра а, при которых неравенство

0

выполняется для всех

IV. Найти все значения параметра а, при которых из неравенства 0.

V. Найти все значения параметра а, при которых выполнение неравенства0.

VI. Найти все значения параметра а, при которых из совокупности неравенств 0.

Перейдем к рассмотрению примеров из материалов вступительных экзаменов.

1. Найти все значения параметра а, при которых из неравенства

0

следует неравенство 0 < x < 1.

Решение.

1) Обозначим символами А множество решений неравенства 0 (1) и В: 0 < x < 1. Требуется выяснить, при каких а справедливо включение

2) Рассмотрим все случаи знака коэффициента а.

2а) a , тогда (1)

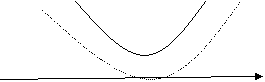
Геометрически:

				x

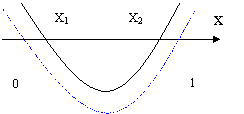
Рис. 1. Рис. 2.

В этом случае множество А есть либо интервал (х1,х2) (рис. 1), либо А = (рис. 2). Поэтому включение выполняется в первом случае, если корни х1, х2 квадратного трехчлена расположены на отрезке , а во втором случае верно всегда (ведь является подмножеством любого множества по определению).

Алгебраически рассмотренный случай записывается в виде совокупности двух систем:

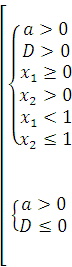
Используя пункты I, II теоремы 7, получаем:

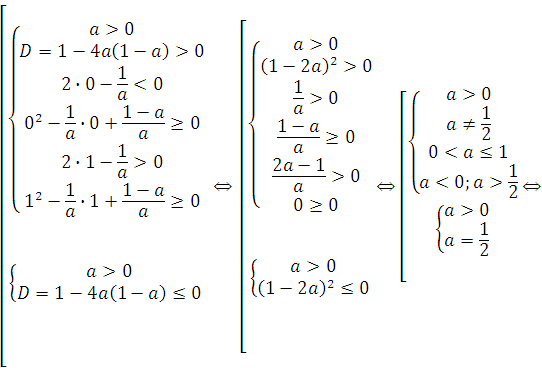
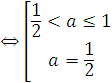
Ответ 2а) .

2б) а = 0 , исходное неравенство (1) принимает вид:

В этом случае множество А: не входит в множество В:

0 < x < 1.

Поэтому

Ответ 2б)

2в) a < , тогда неравенство (1)

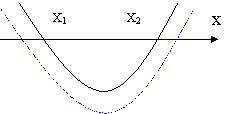
Геометрически:

				x

Рис. 3. Рис. 4.

В случае рис. 3 множество А В случае рис. 4 - А = R. В любом из этих случаев включение очевидно, невозможно. Поэтому

Ответ 2в.

Объединяя ответы из всех трех случаев, получаем:

Ответ. .

II. Найти все значения m, для которых неравенство

0

будет выполняться при всех x > 0.

Решение.

Обозначим через А множество решений неравенства

0 (1), и через В множество x > 0.

Условию задачи соответствует включение

Рассмотрим все случаи знака коэффициента

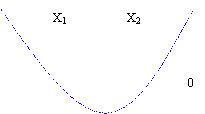
1) , тогда (1)

Геометрически:

			0

 Скачать реферат