Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства

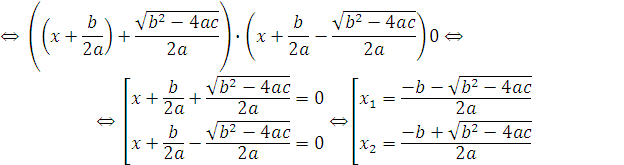
В этом случае уравнение имеет два различных корня:

2) , тогда

в силу (*), то есть - два совпадающих корня.

3) ,

Тогда

не имеет вещественных корней, так как

Итак, доказана теорема:

Теорема 1. Пусть имеется уравнение если

1) , то уравнение не имеет вещественных решений.

2) , то уравнение имеет два равных корня

3) , то уравнение имеет два различных корня

Замечание: если

В этом случае корни удобно находить по формуле

Теорема 2. Если а > 0, то функция монотонно убывает для и монотонно возрастает для

Доказательство теоремы:

Пусть (1),

где произвольные фиксированные числа, тогда из (1) получаем

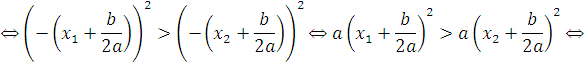
а это по (**) есть , что требовалось доказать.

1) В этом рассуждении использовано монотонное возрастание функции на множестве

2) Докажите, что функция монотонно возрастает на множестве

Аналогично доказывается монотонное возрастание функции на

Теорема 3. Если а < 0, то функция монотонно возрастает для и монотонно убывает для

Доказательство теоремы аналогично доказательству теоремы 2.

Следствие.

Если а > 0, то для любого х

Если а < 0, то для любого х

При а > 0

При а < 0

min и max достигаются при x =.

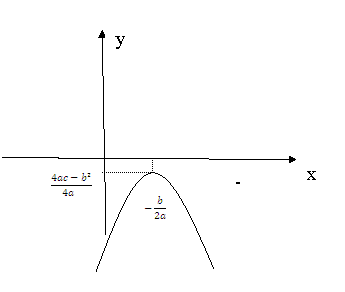
Точка называется вершиной параболы.

1.6 Зависимость расположения графика функций квадратного трехчлена от a, D

Определение. График квадратного трехчлена называется параболой.

Нарисуем эскизы парабол для шести типичных и существенно различных комбинаций значений параметров a и D.

			x

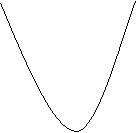
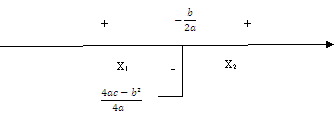2)

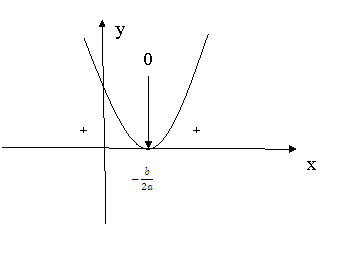
3)

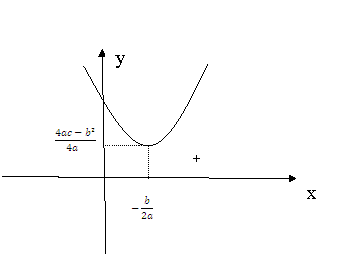
4) )

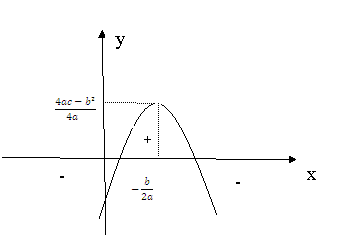
5)

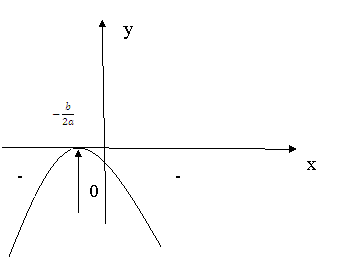
6)

1.7 Решение квадратных неравенств

Опираясь на иллюстрации, сформулируем следующее правило решения квадратных неравенств:

 Скачать реферат