Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства

2) Рассмотрим случай , тогда неравенство (2) равносильно

В этом случае множество А:

	idth=68>
									у
		2				4

и включение неверно.

3) Рассмотрим , тогда неравенство (2) равносильно

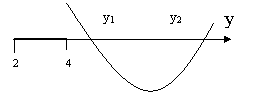
Изобразим графически взаимное расположение множеств А и В, при которых верно включение .

					у

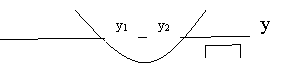Рис. 5.

В случае рис. 3 выполняется система неравенств:

В случае рис. 4 выполняется система неравенств:

В случае рис. 5 выполняется условие D < 0 (8). Из пунктов I, II теоремы 7 следует, что условия (6), (7), (8) равносильны совокупности следующих систем:

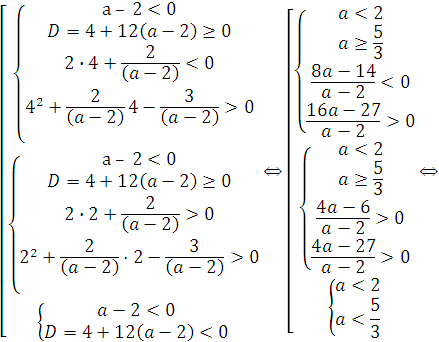
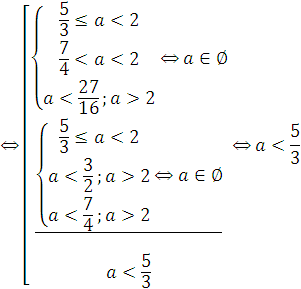
Ответ. .

IV. Найти все значения параметра а, при которых уравнение

=0

имеет по крайней мере два корня, один из которых неотрицателен, а другой не превосходит -1.

Решение.

Найдем область возможных значений параметра, при которых имеет смысл левая часть уравнения.

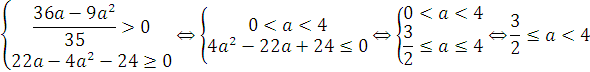
Рассмотрим следующие два случая:

1)

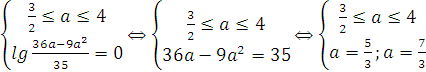
В этом случае любое число является решением уравнения, значит условие задачи выполнено.

Ответ 1)

2) Рассмотрим случай .

В этом случае , и на этот множитель можно сократить, не теряя корней. Итак, при , наше уравнение равносильно следующей системе:

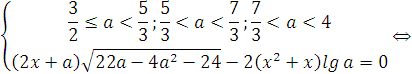
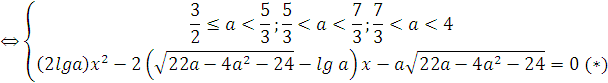
Заметим, что для lg a > lg 1 = 0.

Необходимо выяснить, при каких а из Е справедливы неравенства:

, где - вещественные корни квадратного трехчлена (*).

Иначе говоря, числа -1 и 0 должны находиться между корнями этого квадратного трехчлена.

Согласно пункту III теоремы 7, должна быть справедлива система:

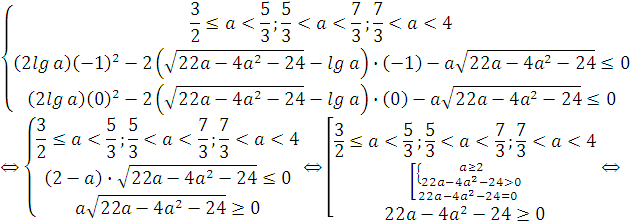
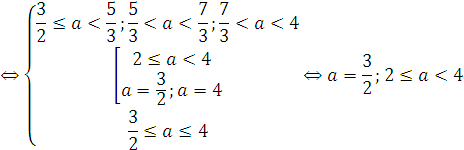
Ответ 2). .

 Скачать реферат