Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства
Ответ. ![]() .
.
2. Найти все значения ![]() , при которых корни уравнения
, при которых корни уравнения ![]() больше
больше ![]() .
.
Решение.
Воспользовавшись пунктом II теоремы 7 получаем: <
p>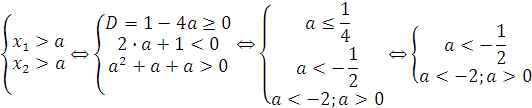
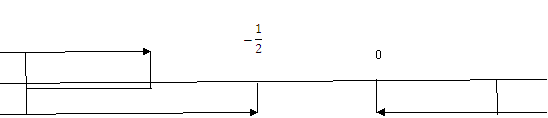
Ответ. a < -2.
3. Найти все значения ![]() , при которых оба корня квадратного уравнения
, при которых оба корня квадратного уравнения
![]() будут меньше 1.
будут меньше 1.
Решение.
Уравнение будет квадратным только если ![]() . В этом случае оно равносильно уравнению:
. В этом случае оно равносильно уравнению:
![]()
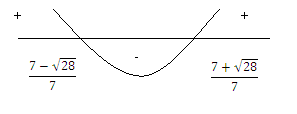
Согласно пункту 1 теоремы 7 получаем, что
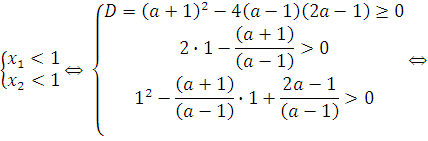
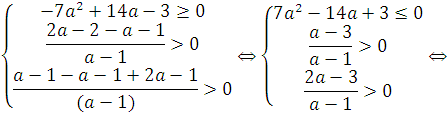
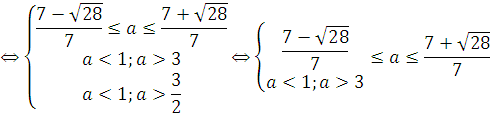
 | |||||||
|
| ||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
|
Ответ. ![]() .
.
Иногда применение теоремы 7 вызывает трудности, так как возникают неравенства третьей или более высокой степени. Тогда, скорее всего, можно выражения для корней исходного квадратного трехчлена получить в виде рациональных функций параметра.
Иными словами:
Если применение теоремы 7, вызывает алгебраические трудности, стоит проверить, не является ли дискриминант рассматриваемого квадратного уравнения полным квадратом. Если дискриминант является полным квадратом, то нужно попытаться выписать выражения для корней и продолжить решение задачи.
4. При каких значениях а все корни уравнения
3a![]() удовлетворяют условию
удовлетворяют условию ![]()
1) Заметим, что если ![]() , то уравнение имеет единственный корень
, то уравнение имеет единственный корень ![]() , и число 0 удовлетворяет условию задачи.
, и число 0 удовлетворяет условию задачи.
2) Если ![]() , то
, то ![]()
Заменим ![]() , тогда
, тогда
![]()
- данное выражение есть полный квадрат! Теперь легко вычислить:
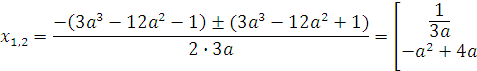
Условие задачи будет выполнено, если справедлива система:
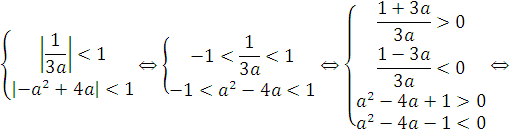
 | ||||||||||||
| ||||||||||||
|
| |||||||||||
 | ||||||||||||
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
