Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства

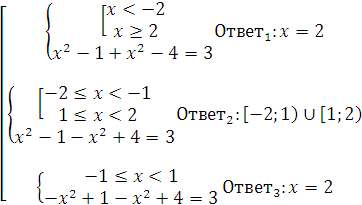
Ответ: .

Такое сокращение рассуждений, во избежание возможных ошибок, мы рекомендуем делать только после приобретения некоторого опыта в решении задач с модулями.

Наиболее полную и наглядную картину дает графическое исследование данного уравнения.

1)

Построим график функции

Для построения будем использовать схему знаков, изображенных на рис. 2. Тогда

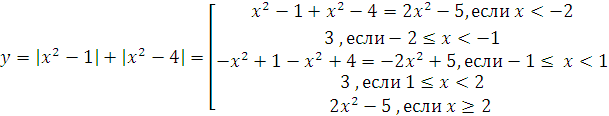
Соответствующий график выглядит так:

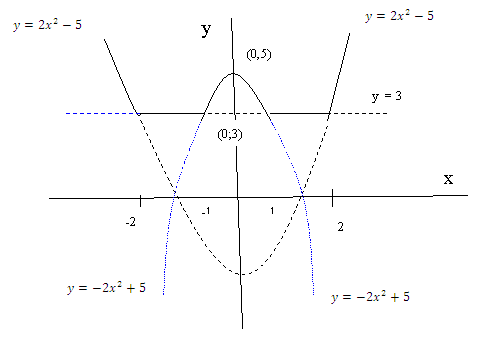Рис. 3.

Построив график правой части уравнения у = 3, убеждаемся, что графики левой и правой части ( и у = 3) пересекаются, а (фактически – совпадают) на множестве и .

Более того, графический подход позволяет сразу же решить обобщенную задачу:

При каждом значении параметра а решить уравнение:

.

Для решения задачи повторим график из рис. 3 и изобразим на том чертеже различные возможные положения прямой у = а.

			у = а, a<0

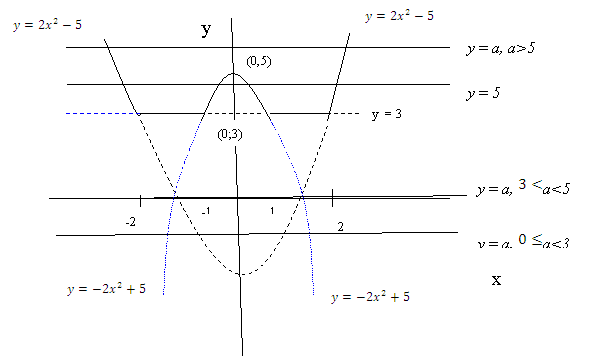Рис. 4.

Выпишем ответ задачи (он непосредственно следует из рис. 4)

Ответ. 1) а < 3 – решений нет;

2) а = 3 – бесконечное множество решений и .

3) 3 < a < 5 – четыре решения:

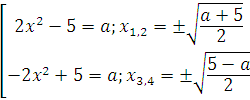
4) a = 5 – три решения:

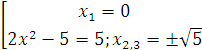
5) a > 5 – два решения:

Приведенная форма решений позволяет сразу же дать ответ для иных возможных постановок задачи.

1) При каких а уравнение

(1)

не имеет решений?

Ответ: а < 3.

2) При каких а уравнение (1) имеет бесконечно много решений?

Ответ: а = 3.

3) При каких а уравнение (1) имеет не менее трех решений?

Ответ: 3а 5.

Пример 2. Определить, при каких значениях а уравнение имеет ровно три корня. Найти эти корни.

Сначала решим данное уравнение, последовательно раскрывая модули в его правой части. Как было указано выше, начнем раскрытие с внутреннего модуля. Для него возможны следующие два случая:

		0

Получаем совокупность двух систем:

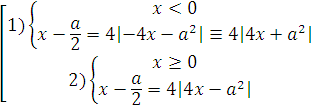
Решим отдельно систему (1) и систему (2).

Диаграмма знаков для системы (1):

Система (1) равносильна, в свою очередь, совокупности двух систем:

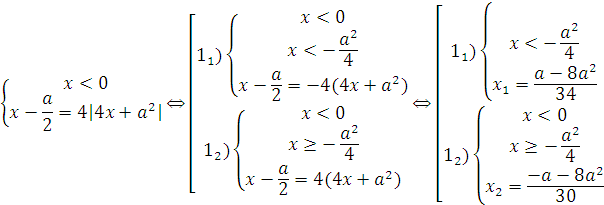
х1 будет решением, если справедливо неравенство

х2 будет решением, если справедлива система:

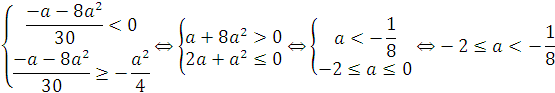
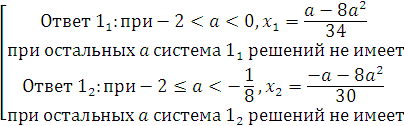
Решаем систему (2) тем же способом:

 Скачать реферат