Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства
![]()
![]()
|
|
|
|
![]()
![]()
Приведенные выше два рисунка иллюстрируют связь параметров k и b с особенностями расположения прямой в декартовой системе координат. В частности, число k = tg α называется угловым коэффициентом прямой.
В данном случае ![]() . Если k = 0, то
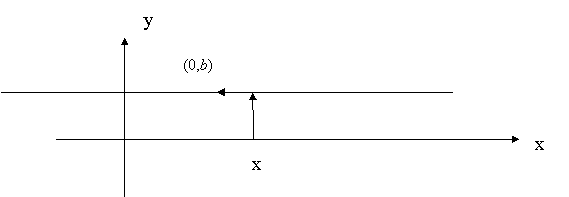
. Если k = 0, то ![]() , линейная функция постоянна и задает прямую, параллельную оси ОХ и | проходящую через точку (0,b) на оси OY.
, линейная функция постоянна и задает прямую, параллельную оси ОХ и | проходящую через точку (0,b) на оси OY.
Перечислим основные свойства линейной функции.
1. Ее областью определения является множество R.
2. Если k ![]() 0 , то множеством значений линейной функции также является множество R, если k = 0, то множество значений — одноточечное множество b.
0 , то множеством значений линейной функции также является множество R, если k = 0, то множество значений — одноточечное множество b.
3. Если k > 0, то ![]() - монотонно возрастающая функция на R, если k < 0, то
- монотонно возрастающая функция на R, если k < 0, то ![]() - монотонно убывает на R.
- монотонно убывает на R.
4. Если b = 0, то ![]() - нечетная функция, у = b - четная функция; если же
- нечетная функция, у = b - четная функция; если же ![]() , то
, то ![]() не является четной или нечетной функцией.
не является четной или нечетной функцией.
Рассмотренные выше случаи не позволяют задать прямую, параллельную оси OY. Поэтому условимся, что уравнение х=х0 задает множество всех точек вида (х0, у), где у ![]() R, то есть задает прямую параллельную оси OY и проходящую че рез точку (хо, 0) на оси ОХ.
R, то есть задает прямую параллельную оси OY и проходящую че рез точку (хо, 0) на оси ОХ.
Чтобы построить прямую, задаваемую уравнением ![]() , достаточно найти две точки (х0, у0) и (х1, у1), удовлетворяющие этому уравнению: у0 = k
, достаточно найти две точки (х0, у0) и (х1, у1), удовлетворяющие этому уравнению: у0 = k![]() х0 + b; у1 = k
х0 + b; у1 = k![]() х1 + b и провести через них искомую прямую.
х1 + b и провести через них искомую прямую.

1.2. Линейные уравнения и неравенства
Рассмотрим простейшее уравнение с двумя параметрами а и b —
линейное а![]() х = b и сразу же выпишем ответ:
х = b и сразу же выпишем ответ:
а![]() х = b
х = b
Ответ:
1) если а ![]() 0, то уравнение имеет единственное решение х0 =
0, то уравнение имеет единственное решение х0 =![]() .
.
2) если ![]() , то решения заполняют всю числовую прямую
, то решения заполняют всю числовую прямую ![]()
3) если ![]() , то нет решений.
, то нет решений.
1.3 Решение линейных неравенств
Сразу же выпишем решения в виде готового правила:
1) а![]() х > b, если a > 0, то x >
х > b, если a > 0, то x > ![]()
если a < 0, то x < ![]()
если a = 0 и b < 0, то x – любое число,
если a = 0 и b![]() 0, то решений нет.
0, то решений нет.
2) а![]() х < b, если a > 0, то x <
х < b, если a > 0, то x < ![]()
если a < 0, то x > ![]()
если a = 0 и b ![]() 0, то решений нет,
0, то решений нет,
если a = 0 и b>0, то x – любое число.
Всегда полезно помнить следующее основное правило:
При умножении или делении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.
При умножении или делении обеих частей неравенства на положительное число знак неравенства не изменяется.
1.4 Квадратный трехчлен
Определение. Квадратным трехчленом называется функция ![]()
Выделение полного квадрата путем тождественных преобразований.
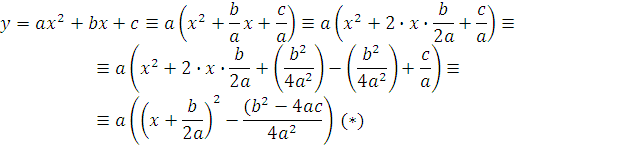
Иначе можно записать в виде:
![]()
Пример 1.
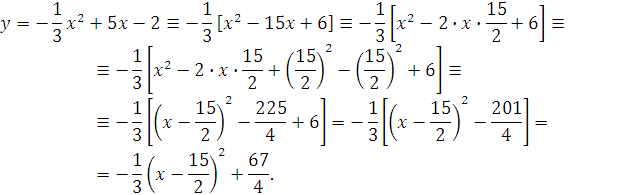
Пример 2.
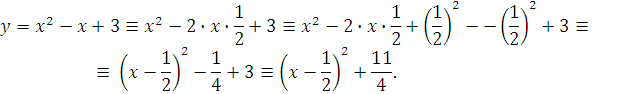
Определение. Число ![]() называется дискриминантом квадратного трехчлена
называется дискриминантом квадратного трехчлена ![]()
1.5 Корни квадратного трехчлена
Нужно найти корни уравнения
![]()
Выделив полный квадрат, получим формулу (*), откуда
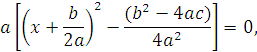
![]()
Мы должны рассмотреть три случая:
1) ![]() , тогда
, тогда
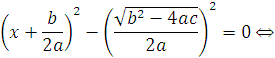
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
