Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства

Рис. 1. Рис. 2.

Включение в случае рис. 1 будет выполняться, если

В случае рис.2

Вновь, используя пункт I теоремы 7, получаем:

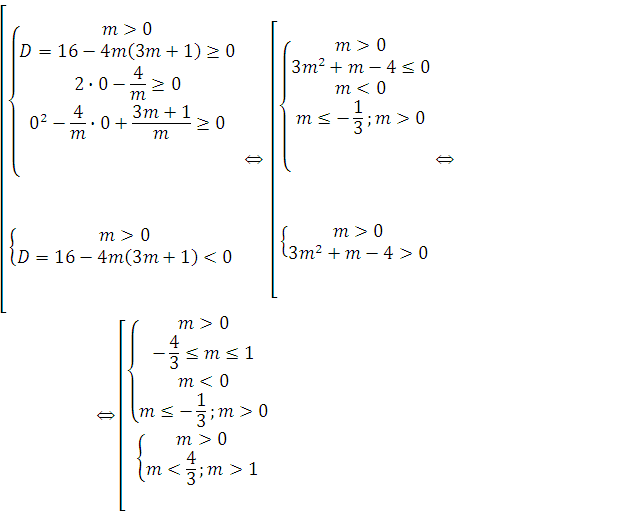
Ответ 1) m > 1.

2) , неравенство (1) принимает вид:

-4

Итак, А: В: х > 0. Очевидно, что включение неверно.

Ответ 2)

3) , тогда (1)

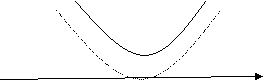
Геометрически:

				x

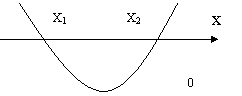Рис. 3. Рис. 4.

В случае рис. 3 в случае рис. 4 А = ; в любом случае невозможно.

Ответ 3)

Ответ. m > 1.

III. При каких значениях параметра а все числа из отрезка удовлетворяют неравенству

Решение.

Обозначим =y

Неравенство (1) в новых обозначениях примет вид:

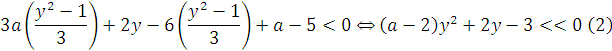
Если , то

Итак, первоначальную задачу можно переформулировать следующим образом.

При каких значениях параметра а из неравенства сдедует неравенство

Как и ранее, обозначим через А множество решений неравенства и В: Требуется определить, при каких а справедливо

Рассмотрим все случаи знака коэффициента (а - 2).

1) , тогда неравенство (2) равносильно

Воспользовавшись геометрическим подходом, получаем:

						у

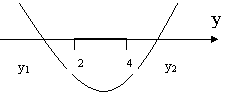Рис. 1. Рис. 2.

В случае рис. 1 множество А: . В случае рис. 2 множество А = .

Включение возможно, только если числа 2 и 4 лежат между корнями квадратного трехчлена.

Из пункта III теоремы 7 следует система:

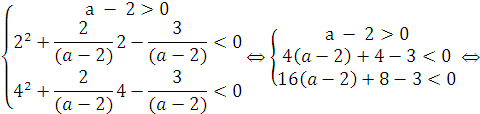
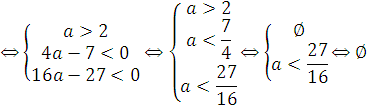
Ответ 1) .

 Скачать реферат