Линейные и квадратичные зависимости, функция х и связанные с ними уравнения и неравенства
|
|

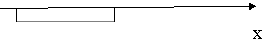 | |||||
 | |||||
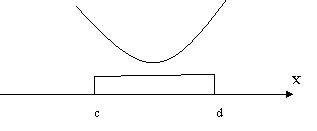 | |||||
Рис. 5.
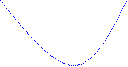
Алгебраически: рис. 3 – квадратный трехчлен имеет корни, расположенные правее числа d (возможно х1 = d); рис. 4 - квадратный трехчлен имеет корни, расположенные левее числа с (возможно х2 = с); рис. 5 - квадратный трехчлен не имеет корней.
Пользуясь теоремой 7 пункты I, II, выпишем вышесказанное в виде совокупности алгебраических систем:
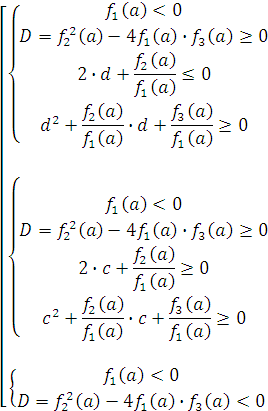
Полный ответ задачи получается объединением ответов из случаев 1); 2); 3).
Теперь ясно, что:
Решая задачу о взаимном расположении решений квадратных неравенств с логическим высказыванием, удобно поступить следующим образом:
1) переформулировать логическое высказывание на языке теории множеств, в виде соотношений включения для множества решений неравенств.
2) получить геометрические иллюстрации, которые выясняют возможное взаимное расположение границ множеств решений – корней квадратных трехчленов.
3) выписать, используя результаты теоремы 7, совокупность алгебраических систем, которые соответствуют различным случаям геометрического расположения корней и различным случаям знака коэффициента при х2 в неравенствах.
4) собрать в окончательном ответе задачи объединение промежуточных ответов для всех рассмотренных случаев.
Применим сформулированный алгоритм, для решения следующей задачи:
II. Найти все значения параметра а, при которых неравенство:
![]() 0 (6)
0 (6)
выполняется для всех ![]()
Решение.
1) Если А – множество решений неравенства (6), В – множество (7), то задача соответствует включению ![]() .
.
2) Разберем все возможные случаи знака коэффициента ![]() , и для каждого из них приведем геометрические иллюстрации:
, и для каждого из них приведем геометрические иллюстрации:
2а) ![]() , тогда (6)
, тогда (6) ![]()
 | |||||
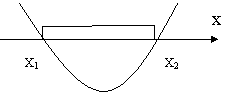 | |||||
| |||||
Рис. 1. Рис. 2.
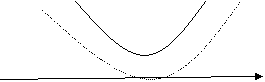
В этом случае множество А – либо интервал (х1,х2) (рис. 1), либо А = ![]() (рис. 2). Поэтому включение
(рис. 2). Поэтому включение ![]() невозможно.
невозможно.
2б) ![]() , тогда неравенство (6) примет вид:
, тогда неравенство (6) примет вид: ![]()
Изобразим графически различные возможные варианты расположения прямой ![]() для этого случая (4 рисунка).
для этого случая (4 рисунка).
 | |||
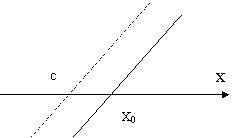 | |||
Рис. 3. Рис. 4.
 | |||
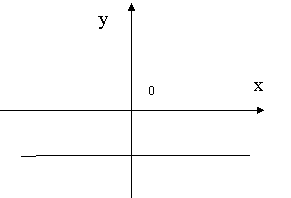 | |||
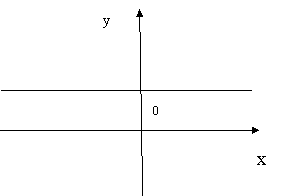
Рис. 5. Рис. 6.
На рис. 3 и рис. 5 множество А = (-![]() и А =
и А = ![]() - соответственно.
- соответственно.
На рис. 4 и рис. 6 множество А = (![]() и А =
и А = ![]() - соответственно.
- соответственно.
Ясно, что включение ![]() возможно только в случаях рис. 3 и рис. 5.
возможно только в случаях рис. 3 и рис. 5.
Алгебраически это соответствует:
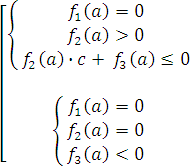
2в) ![]() , тогда неравенство (6) запишется в виде:
, тогда неравенство (6) запишется в виде:
![]()
Возможны два различных случая расположения параболы
![]()
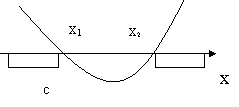 | |||||
 | |||||
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
