Учение о параллельности. Открытие неевклидовой геометрии

Введение

Эвклид – древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике. Биографические сведения о жизни и деятельности Эвклида крайне ограничены. Известно, что он родом из Афин, был учеником Платона. Научная деятельность его протекала в Александрии, где он создал математическую школу.

Достижения в математике

Главные труд

ы Эвклида «Начала» (латинизированное назв. – «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел, алгебры, общей теории отношений и метода определения площадей и объемов, включающего элементы пределов (Метод исчерпывания). В «Началах» Эвклид подытожил все предшествующие достижения греческой математики и создал фундамент для ее дальнейшего развития. Историческое значение «Начал» Эвклида заключается в том, что в них впервые сделана попытка логического построения геометрии на основе аксиоматики. Основным недостатком аксиоматики Эвклида следует считать ее неполноту; нет аксиом непрерывности, движения и порядка, поэтому Эвклиду часто приходилось апеллировать к интуиции, доверять глазу. Книги XIV и XV являются более поздними добавлениями, но являются ли первые тринадцать книг созданием одного человека или школы, руководимой Эвклидом, не известно. С 1482 г. «Начала» Эвклида выдержали более 500 изд. на всех языках мира.

Первые четыре книги «Начал» посвящены геометрии на плоскости, и в них изучаются основные свойства прямолинейных фигур и окружностей.

Книге I предпосланы определения понятий, используемых в дальнейшем. Они носят интуитивный характер, поскольку определены в терминах физической реальности: «Точка есть то, что не имеет частей». «Линия же – длина без ширины». «Прямая линия есть та, которая равно расположена по отношению точкам на ней». «Поверхность есть то, что имеет только длину и ширину» и т.д.

За этими определениями следуют пять постулатов: «Допустим:

1) что от всякой точки до всякой точки можно провести прямую линию;

2) и что ограниченную прямую можно непрерывно продолжить по прямой;

3) и что из всякого центра и всяким раствором может быть описан круг;

4) и что все прямые углы равны между собой;

5) и если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные неограниченно эти две прямые встретятся с той стороны, где углы меньше двух прямых».

Три первых постулата обеспечивают существование прямой и окружности. Пятый, так называемый постулат о параллельных – самый знаменитый. Он нарочито чужероден, его громоздкая формулировка закономерно вызывает некоторое чувство протеста и желание отыскать для него доказательство, он всегда интриговал математиков, которые пытались вывести его из четырех предыдущих или вообще отбросить. Такие доказательства уже в древности пытались построить Птолемей и Прокл; а в Новое время из этих попыток развилась неевклидова геометрия. Следует отметить, что первые 28 теорем I книги относятся к абсолютной геометрии и в XIX в. обнаружилось, что можно построить другие, неевклидовы геометрии и что пятый постулат имеет право на существование.

Начала Евклида

Начала – главный труд Евклида, написанный около 300 г. до н.э. и посвящённый систематическому построению геометрии. Начала – вершина античной геометрии и античной математики вообще, итог её 300-летнего развития и основа для последующих исследований.

Прокл сообщает, что подобные сочинения создавались и до Евклида: Начала были написаны Гиппократом Хиосским, а также платониками Леонтом и Февдием. Но эти сочинения, по-видимому, были утрачены ещё в античности.

Текст Начал на протяжении веков были предметом дискуссий, к ним написаны многочисленные комментарии. Из античных комментариев до нас дошёл комментарий, написанный Проклом. Этот текст является важнейшим источником по истории и методологии греческой математики. Прокл дает краткое изложение истории греческой математики (т. н. Евдемов каталог геометров), обсуждает взаимосвязь метода Евклида и логики Аристотеля, роль воображения в доказательствах.

Из древних комментаторов следует упомянуть Паппа, из новых – Пьера Рамуса, Федериго Коммандино, Христофа Шлюсселя (Клавиуса) и Савилия.

Начала оказали огромное влияние на развитие математики вплоть до Новейшего времени. Книга переведена на множество языков мира. Так, на китайском языке первые 6 книг Начал издал Маттео Риччи во время своей миссии в Китае (1583–1610). По количеству переизданий Начала не имеют себе равных среди светских книг.

Альберт Эйнштейн так оценивал Начала: «Это удивительнейшее произведение мысли дало человеческому разуму ту уверенность в себе, которая была необходима для его последующей деятельности. Тот не рожден для теоретических исследований, кто в молодости не восхищался этим творением».

В Началах излагаются планиметрия, стереометрия, арифметика, отношения по Евдоксу. В классической реконструкции Гейберга весь труд состоит из 13 книг. К ним традиционно присоединяют две книги о пяти правильных многогранниках, приписываемые Гипсиклу Александрийскому и школе Исидора Милетского.

Изложение в Началах ведётся строго дедуктивно. Каждая книга начинается с определений. В первой книге за определениями идут аксиомы и постулаты. Затем следуют предложения, которые делятся на задачи (в которых нужно что-то построить) и теоремы (в которых нужно что-то доказать). Определения, аксиомы, постулаты и предложения пронумерованы, напр., I def. 2 – второе определение первой книги.

Первая книга

1. Первая книга начинается определениями, из которых первые семь (I def. 1–7) гласят: Точка есть то, что не имеет частей.

2. Линия – длина без ширины.

3. Края же линии – точки.

4. Прямая линия есть та, которая равно лежит на всех своих точках.

5. Поверхность есть то, что имеет только длину и ширину.

6. Края же поверхности – линии.

7. Плоская поверхность есть та, которая равно лежит на всех своих линиях.

Комментаторы эпохи Возрождения предпочитали говорить, что точка есть место без протяжения. Современные авторы, напротив, признают невозможность определения основных понятий, и Давид Гильберт начинает «Основания геометрии» так:

Мы мыслим три различные системы вещей: вещи первой системы мы называем точками и обозначаем

За определениями Евклид приводит постулаты (I post. 1–5):

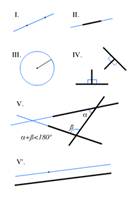
1. От всякой точки до всякой точки можно провести прямую.

2. Ограниченную прямую можно непрерывно продолжать по прямой.

3. Из всякого центра всяким раствором может быть описан круг.

4. Все прямые углы равны между собой.

5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

 Скачать реферат