Методические рекомендации к уроку "Сложное отношение точек. Полный четырехвершинник"

Следствие. При любом проективном отображении одной прямой на другую сложное отношение четырех точек сохраняется.

Теорема 2. Если биекция сохраняет сложное отношение любой четверки точек, то – проективное отображение.

Доказательство. Пусть height=25 src="images/referats/29601/image089.png">– различные точки прямой и их образы в отображении . Существует единственной проективное отображение , которое переводит точки в точки соответственно.

Если , и , то по доказанному

.(3)

Если , то по условию

(4)

(3), (4)

и, значит, точки и совпадают. Так как , то такой вывод справедлив для любой точки . Следовательно, данное нам отображение совпадает с проективным отображением . Теорема доказана.

Следствие. Биекция является проективным отображением тогда и только тогда, когда она сохраняет сложное отношение любой четверки точек.

Теорема 3. Пусть – четыре различные прямые пучка П(О), прямая не проходит через точку и – точки пересечения этой прямой с прямыми . Тогда сложное отношение не зависит от выбора прямой (оно называется сложным отношением четырех названных прямых).

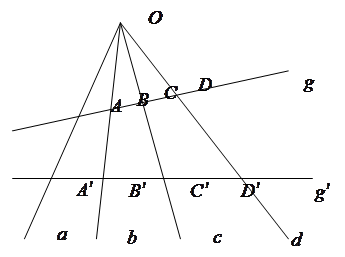
Рис. 2

Доказательство. Проведем еще какую-либо прямую , она пересекается с прямыми в точках соответственно (рис 2). Пучок П(О) устанавливает перспективное отображение по закону: . Так как это частный случай проективного отображения, то . Теорема доказана.

Следствие. Биекция :П()П() одного пучка на другой является проективным отображением тогда и только тогда, когда она сохраняет сложное отношение любой упорядоченной четверки прямых.

Сложное отношение точек заданных своими координатами на проективной плоскости

Как найти сложное отношение четырех точек прямой , зная их координаты , , , относительно репера на плоскости?

Прямая не проходит по крайней мере через одну из точек . Для определенности будем считать, что (рис. 3).

Рассмотрим перспективное отображение с помощью пучка прямых П(). Имеем:

. (5)

В репере на прямой имеем координаты точек:

.

Поэтому

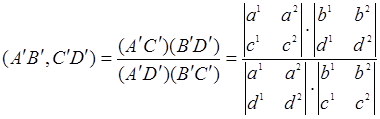
и, учитывая равенство (5),

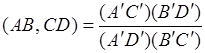. (6)

Аналогичные выражения получим, если прямая не проходит через вершину или координатного треугольника, проектируя точки прямой на из или на и из .

На проективной плоскости возьмем репер и произвольную точку . Пусть – проекции точек и на прямую из центра . Мы знаем, что в репере на прямой точка имеет координаты и, следовательно, по формуле (2) 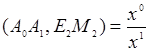при условии, что , то есть . Аналогичные выражения получим и для других отношений между координатами точки . Поэтому справедлива