Методические рекомендации к уроку "Сложное отношение точек. Полный четырехвершинник"

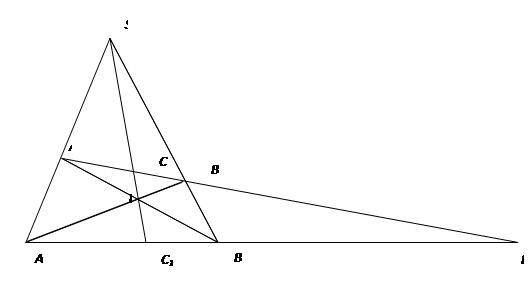
Рис.16

Замечание. Если бы прямые и были параллельны, то и прямая была бы им параллельна. Это означало бы, что центр S перспект

ивы бесконечно удален. Такой случай мы считаем вырожденным и не рассматриваем.

На основе доказанного утверждения можно решить, например, задачу о трех окружностях.

Задача 1. Докажите, что внешние центры гомотетий трех окружностей лежат на одной прямой.

Доказательство. Пусть даны окружности с центрами . Обозначим внешние центры гомотетий буквами , а внутренние центры – буквами .

Четверки точек и являются гармоническими и имеют общую точку , значит для них существует центр перспективы (утверждение 2). Итак, прямые должны пересекаться в одной точке и это точка . Следовательно, внешние центры гомотетий расположены на одной прямой.

Занятие 4. Четырехвершинник

Выделим на рис. 16 фигуру состоящую из четырех точек – (никакие три из них не лежат на одной прямой!) и шести прямых – . Эта фигура называется четырехвершинником . Указанные точки называются его вершинами, а прямые – сторонами. Четырехвершинник легко построить путем проведения прямых через все пары отмеченных вершин.

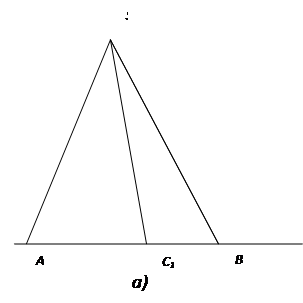
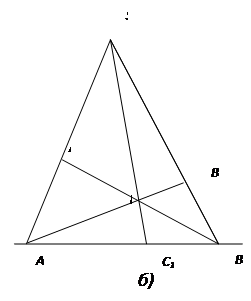
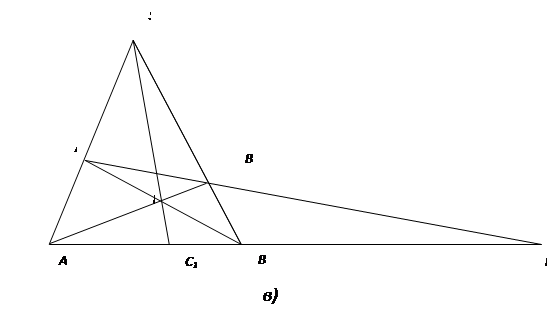
Рис. 17

Замечание. На практике построение произвольного четырехвершинника удобно начинать не с вершин (иначе некоторые прямые могут пересечься за пределами чертежа), а с двух сторон и вспомогательной прямой . И далее следовать представленной на рис. 17 схеме.

Утверждение 3. В любом четырехвершиннике, построенном по указанной на рис. 17 схеме, четверка точек получится гармонической.

Доказательство. На рис. 16 четверка точек проектируется из центра в четверку точек . Согласно замечанию 2 (занятие 2),

.

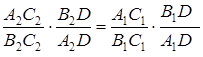В четверку точек также проектируется, но уже из центра , четверка точек (обратите внимание на порядок точек в этом случае!). Имеем:

.

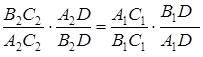Перемножав почленно левые и правые части этих равенств, получим

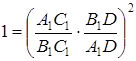, откуда .

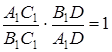Следовательно, четверка точек – гармоническая.

Покажем теперь, как отмеченное свойство четырехвершинника применяется при решении задач планиметрии.

Задача 2. Точка O принадлежит высоте треугольника ABC и находится внутри него. Прямые AO и BO пересекают стороны треугольника в точках E и K. Докажите, что углы KHC и EHC равны.

Доказательство. Пусть и . Покажем, что .

Проведем прямую KE и обозначим точку её пересечения с прямой AB буквой P (рис. 18).

Рис. 18

Рассмотрим четырехвершинник . Так как четверка точек – гармоническая (утверждение 3), то и проектирующие её из центра H прямые HK, HE, HM, HP составляют гармоническую четверку, поэтому, согласно замечанию 1 (занятие 2),

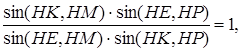
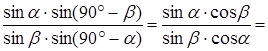
=1.

Итак, , а так как углы острые, то .

Если прямые KE и AB параллельны, то к точкам A, B и H четвертой гармонической будет бесконечно удаленная точка. В этом случае H – середина отрезка AB и из свойств осевой симметрии следует равенство углов и .

Замечание. Из доказанного в задаче 2 утверждения следует, что если серединные перпендикуляры к сторонам треугольника пересекаются в точке O, расположенной внутри треугольника, то она является одновременно точкой пересечения высот в треугольнике и точкой пересечения биссектрис в треугольнике .

Задачи для самостоятельной работы

1. На прямой отмечены точки A, B и C. Постройте четвертую гармоническую к ним точку D, если точка C:

а) лежит между точками A и B и AC>BC;

б) лежит вне отрезка AB;

в) является серединой отрезка AB.

2. Докажите, что пересекающиеся прямые a и b гармонически разделяются прямыми c и d, содержащими биссектрисы образовавшихся при пересечении углов.

3. Докажите, что на рис.19 любая четверка точек, принадлежащих одной прямой, – гармоническая.