Методические рекомендации к уроку "Сложное отношение точек. Полный четырехвершинник"

Решение:

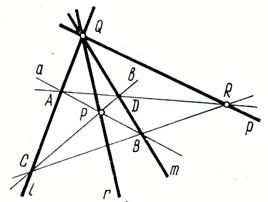
Рис. 6

Обозначим прямую через . Рассмотрим полный четырёхвершинник . Его диагональными точками являются h=49 height=21 src="images/referats/29601/image301.png">, прямые и – две его диагонали. Так как, через каждую диагональную точку полного четырёхвершинника проходит гармоническая четверка прямых, то есть пара прямых гармонически разделяет пару прямых . Отсюда следует, что как только заданные прямые и точка , так однозначно определяется третья прямая , а затем и четвёртая гармоническая прямая . Итак, прямая зависит только от и , но не от и .

Задача №10.

Построены диагональные точки полного четырехвершинника : , , . Точки определены соотношениями: пара точек гармонически разделяет пару точек ; – разделяет ; – разделяет . Доказать, что: 1) прямые сходятся в одной точке ; 2) пара точек гармонически разделяет пару точек

Решение:

1) Рассмотрим полный четырехвершинник . Его диагональными точками являются и . Диагональ пересекает сторону четырехвершинника в точке, четвертой гармонической к . Но согласно условию, гармонически разделяет ; значит, прямая проходит через точку , а поэтому и через . Итак, прямые и действительно сходятся в точке .

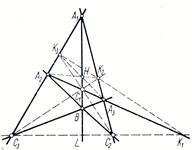
Рис. 7

2) Рассмотрим полный четырехвершинник . Точки и – его диагональные точки, прямая – диагональ. Она пересекает противоположные стороны и , проходящие через третью диагональную точку, в точках и соответственно; следовательно в силу того, что на каждой диагонали полного четырехвершинника имеется гармоническая четверка точек, пара точек гармонически разделяет пару точек .

Задача №11.

На прямой даны три точки . Пользуясь одной линейкой, построить четвертую гармоническую точку .

Решение:

Будем считать плоскость чертежа евклидовой плоскостью, поэтом различим два случая.

1) Точка лежит вне отрезка (рис 8, а).

Будем считать и вершинами некоторого полного четырехвершинника, а – его диагональной точкой. Возьмем вне прямой точку (вторая диагональная точка). Построим и (пара противоположных сторон). Из точки (которая пока без пары) проведем к треугольнику секущую ( и – третья и четвертая вершины; лежит на , – на ).