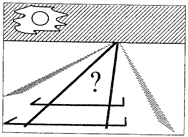
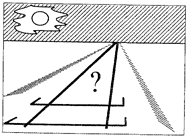
Методические рекомендации к уроку "Сложное отношение точек. Полный четырехвершинник"

Пусть и – точки пересечения диагонали с противоположными сторонами и , п

роходящими через третью диагональную точку . Докажем, что

. (7)

Проектируя точки , , , на прямую из центра , получим:

. (8)

Проектируя точки , , , на прямую из центра , получим:

(9)

(2), (3)(10)

Но по второму свойству §1

,(11)

(4), (5)

Но при точки и совпадают, а следовательно, совпадают прямые и , и точки , , , оказываются на одной прямой, что противоречит условию. Поэтому

,

(6)

(7)

Заметим, что в полном четырехвершиннике все его вершины равноправны, как равноправны все его диагональные точки. Поэтому справедлива

Теорема 5. Полный четырехвершинник обладает следующими свойствами:

1) на каждой диагонали имеется гармоническая четверка точек, в которой одной парой служат диагональные точки, а другой парой – точки пересечения этой диагонали со сторонами, проходящими через третью диагональную точку;

2) на каждой стороне имеется гармоническая четверка точек, в которой одной парой служат вершины, а другая пара образована диагональной точкой и точкой пересечения этой стороны с диагональю, проходящей через две другие диагональные точки;

3) через каждую диагональную точку проходит гармоническая четверка прямых, в которой одной парой служат противоположные стороны, а другой диагонали.

Первый пункт этой теоремы дает способ построения четвертой гармонической точки к упорядоченной тройке точек , , . Через точку проводим произвольную прямую , а через точку – две произвольные прямые и . Обозначим:

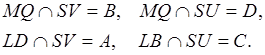
Тогда искомая.

3.Итог занятия.

Итак, сегодня на занятии мы ввели понятие гармонической четверки, изучили теорему о свойствах полного четырехвершинника.

– Когда четыре точки лежащие на одной прямой, называют гармонически расположенными?

Возможный вариант ответа: Если сложное отношение четырёх точек прямой равно минус единице.

Далее, в подведении итогов лекции, студентам предлагается решить следующую задачу:

Даны отрезок , его середина C и точка M, не лежащая на прямой . С помощью одной линейки построить прямую, проходящую через точку M и параллельную прямой .

После нескольких минут самостоятельного решения задачи, к доске вызывается студент либо по собственному желанию, либо на усмотрение преподавателя. Далее задача решается студентом с помощью аудитории.

2.3 Тематический план и методические рекомендации к проведению практических занятий

Практические занятия чаще всего являются продолжением лекционных форм обучения и служат для осмысления и более глубокого изучения теоретических проблем, а также отработки навыков использования знаний. Практическое занятие даёт студенту возможность проверить, уточнить, систематизировать знания, овладеть терминологией и свободно его оперировать, научиться точно и доказательно выражать свои мысли на языке конкретной науки, анализировать факты, вести диалог, дискуссию, оппонировать. Практика призвана укреплять интерес студента к науке и научным исследованиям, научить связывать научно – теоретические положения с практической деятельностью[15].

На практических занятиях студенты проверяют, насколько тесно теория связана с практикой и осознают её необходимость для будущей профессиональной деятельности. По сути дела, практическое занятие и его результаты есть ничто иное как проявление принципа обратной связи на вузовском этапе профессиональной подготовки.