Методические рекомендации к уроку "Сложное отношение точек. Полный четырехвершинник"

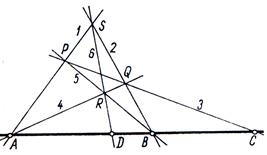
Рис 8, а

Построим прямые и ; получим точку (третья диагональная точка). Наконец, построим прямую (диагональ) и получим точку . В силу того, что на каждой стороне полного четырехвершинника имеется гармоническая четверка точек, получаем – пара точек гармонически разделяет пару точек .

Точка не зависит от выбора точки и секущей .

2) Точка лежит внутри отрезка (рис 8, б)

Снова будем считать и вершинами некоторого полного четырехвершинника, но теперь диагональной точкой будем считать не , а искомую точку .

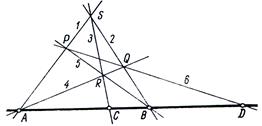
Рис 8, б

Возьмем вне прямой точку (диагональная точка). Построим прямые и (пара противоположных сторон и диагональ). На прямой возьмем точку (вторая диагональная точка) и построим прямые и (пара противоположных сторон); получим точки и (третья и четвертая вершины). Наконец, построим прямую (сторона, противоположная ) и получим точку (третья диагональная точка). В силу того, что на каждой стороне полного четырехвершинника имеется гармоническая четверка точек, получаем, что пара точек гармонически разделяет пару точек .

Как в первом, так и во втором случае мы строим одну и ту же фигуру. Разница заключается лишь в очередности построения прямых и .

Задача №12.

Даны три прямые пучка (рис. 9). Пользуясь одной линейкой, построить четвертую гармоническую прямую .

Решение:

Будем считать и парой противоположных сторон некоторого полного четырехвершинника, а – его диагональю. Тогда центр пучка будет диагональной точкой этого четырехвершинника, а искомая прямая будет второй диагональю, проходящей через , так как через каждую диагональную точку полного четырехвершинника проходит гармоническая четверка прямых.

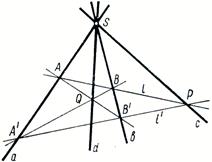
Рис. 9

Возьмем на прямой точку (вторая диагональная точка). Проведем из к углу две секущие (вторая пара противоположных сторон). Мы получим четыре точки: (вершины). Построим прямые и (третья пара противоположных сторон) и получим точку (третья диагональная точка). Прямая (диагональ) и есть искомая прямая .

Задача №13.Найти координаты точки С в репере на прямой, если в этом репере: A(2;3), В(-1;1), D(-3;5), а сложное отношение

Задача №14.Три точки прямой заданы своими аффинными координатами: A(5;12), B(9;3), C(10;7). Найти на этой прямой точку D(x;y), удовлетворяющую условию .

Задача №15Построены диагональные точки полного четырехвершинника : , , . Точки определены соотношениями: пара точек гармонически разделяет пару точек ; – разделяет ; – разделяет . Доказать, что: 1) прямые сходятся в одной точке ; 2) пара точек гармонически разделяет пару точек