Методические рекомендации к уроку "Сложное отношение точек. Полный четырехвершинник"

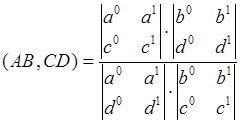. (1)

Коротко можно записать так 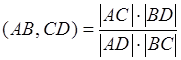, где определитель составленный из координат точек и .

Сложное отношение точек не зависит от выбора проективного репера. Если – собственные точки прямой, то выполняется равенство:

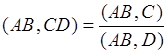. (2)

Пусть точки имеют координаты: , , . Поскольку проективные координаты определяются с точностью до проективного множества, то можно считать, что эти точки имеют координаты:

, , , . (*)

Где 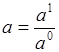, ,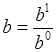,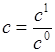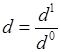. Поскольку, сложное отношение точек не зависит от выбора репера, то в качестве репера можно выбрать репер , тогда будут являться аффинными координатами на данной прямой.

Найдем простое отношение (используя определение простого отношения): , .

Найдем сложное отношение по формуле (1), используя координаты (*):

.

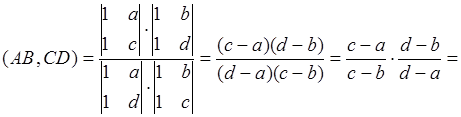
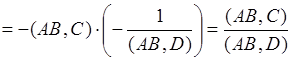Замечание 1. Несобственная точка делит любой отрезок прямой в отношении , то есть .

Замечание 2. Если выбрать в качестве репера , то в этом репере точка будет иметь координаты: . Зная сложное отношение точек , всегда можно найти расположение точки на прямой. В этом случае .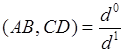

Значит, если , то .

Свойства сложного отношения четырех точек

10: Сложное отношение точек не изменится, если поменять местами пару точек: .

Доказательство: 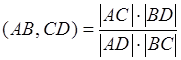, 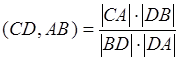. Учитывая, что получим, что . Свойство доказано.

20: Сложное отношение точек меняет свое значение на обратное, при перестановке точек внутри одной пары: .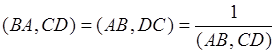

Доказательство: 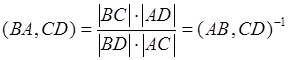, 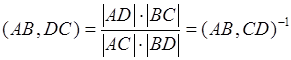. Свойство доказано.

30: Если поменять местами точки внутри каждой пары, то сложное отношение не изменится: .

Доказательство: следует из свойства 20. 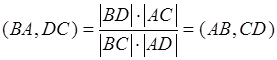. Свойство доказано.

40: .

Доказательства первого, второго и третьего свойства предложить студентам на самостоятельное изучение.

Замечание. Пусть на прямой заданы точки , тогда

1) тогда и только тогда, когда точки ,

2) тогда и только тогда, когда точки .

Теоремы о сложном отношении точек и прямых

Теорема 1. При любом проективном преобразовании плоскости сложное отношение четырех точек прямой сохраняется.

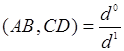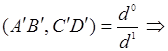
Доказательство. Пусть – проективное преобразование плоскости , прямая , ; точки переходят в отображении в точки . Как мы знаем, сужение есть проективное отображение . Это отображение вполне определяется упорядоченной парой реперов , где , . Если – координаты точки в репере , то эти же координаты имеет точка в репере . Но , . Теорема доказана.