Доказательство утверждения, частным случаем которого является великая теорема Ферма

Откуда (11) - нечетное число при - нечетном и - четном, т.к. , причем (12) (явно) при .

********

Вывод:

На основании (8) и (11) имеем: (13) - нечетное число;

из соотношений (7) и (12) имеем: (14) (явно) при .

Это дополнительная информация о свойствах предполагаемых взаимно простых числах , которая в дальнейшем нам очень пригодится.

*******

Теперь попробуем выразить сумму квадратов чисел c и . Учитывая соотношения (9) и (10), получим:

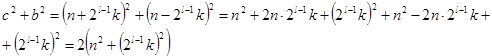
Таким образом, получили следующее уравнение:

(15),

где - целые числа, которые, являясь решениями уравнения (15), в свою очередь, могут быть выражены через другие целые числаследующим образом:

(16) - нечетное число при - нечетном;

(17) - нечетное число при - нечетном;

(18) - нечетное число при - нечетном;

(19) - четное число.

Примечание: во всех последующих исследованиях (Случаях) нас не будут интересовать

t =0 иr=0 (при t =0 и - четные из (16) и (17), при r=0 = 0 (из (19)) => а = 0 (из (6)), что противоречит нашему допущению).

*******

Примечание.

Общий вид уравнения (15) следующий:

(20) ,

целыми решениями которого (это известный факт в теории чисел) являются:

(21) ;

(22) ;

(23) ;

(24) , где - целые числа.

То, что (21), …, (24) являются решениями уравнения (20), легко проверяется их подстановкой в данное уравнение (20), которое при этом превращается в тождество.

*******

Для простоты обозначим правые части уравнений (16), …, (19) буквами С, В, N, К, т.е.

= С

= В

= N

= К,

и рассмотрим случай, когда в правых частях уравнений (16), …, (19) перед С, В, N, К, стоят «плюсы» и выполняется Условие 1.

Условие1 (начало).

с = С

b = B

n = N

Случай «+».

(16+) = С - нечетное число при - нечетном;

(17+) = В - нечетное число при - нечетном;

(18+) = N - нечетное число при - нечетном;

(19+) = К - четное число.

Казалось бы, все в порядке: четность в (16+), …, (19+) совпадает при -нечетном с нашими предыдущими рассуждениями.

Однако не все так просто.

Помимо всего прочего, у нас есть еще две дополнительные информации (13) и (14) (о четности, заключенной в «Выводе» (стр.5)), вытекающие из предположения о том, что, вопреки условию «Утверждения 1», допустим, существуют попарно взаимно простые целые числа .

Попробуем найти сумму , воспользовавшись их выражениями (16+) и (17+):

,

т.е. пропорционально 4, откуда следует, учитывая (13) в «Выводе» (стр.5), !

Т.е., вопреки «Выводу», в Случае «+» является не нечетным, а четным числом, что возможно (из (18+)) при -четном.

Однако, если - четное, то (в (16+) и (17+)) являются четными, т.е. в уравнениях (2) и (1) числа - четные, а потому не являются попарно взаимно простыми целыми числами.

 Скачать реферат