Доказательство утверждения, частным случаем которого является великая теорема Ферма

Теперь, с учетом (17′) и (18), найдем сумму :

т.к. , т.е. .

(Здесь чередование «плюса» и «минуса»

такое же, как и у единицы в (29). В последующих действиях мы это учтем).

Теперь, учитывая (32), получим значение для b:

, т.к. из (29) вытекает .

Итак, .

Учитывая (35´), получим => ().

Теперь, с учетом (), можно получить окончательное выражение для с (из (34´)):

, т.е. (39´´).

Таким образом, уравнение (15), решениями которого являются (16), (17′), (18) и (19´), в конечном счете имеет следующие решения:

(39´´),(38´´), где - взаимно простые нечетные

, (33´), целые числа.

********

Случай 4

Нетрудно догадаться, что если бы у уравнения (15) были бы решения, противоположные по знаку с решениями (16), (17′), (18) и (19´), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (39´´), (37), (38´´) и (33´), т.е.

(39´´´),(38´´´), (37´), (33),

где - взаимно простые нечетные целые числа.

*******

Подведем некоторый итог. Нами рассмотрено 4 случая решений уравнения (15).

Ранее мы обозначили правые части уравнений (16),…, (19) буквами С, В, N, К, т.е

= С

= В

= N

= К

Тогда эти первые 4 случая следующие:

1. (16) 2. (16´) (39´)

(17´) (37) (17) (37´)

(18) (18´) (38´)

(19) (33) (19´) (33´)

3. (16) (39´´) 4. (16´) (39´´´)

(17´) (37) (17) (37´)

(18) (38´´) (18´) (38´´´)

(19´) (33´) (19) (33)

*********

Рассмотрим еще 10 случаев.

5. с = С 6. с = - С 7. c = C 8. c = - C

b = - B b = B b = - Bb = B

n= - N n = N n = - Nn = N

9. с = С. 10. с = -С 11. с = С 12. с = -С

b = B b = -B b = B b = -B

n =- N n = N n = N n =- N

13. с = С 14. с = -С

b = B b =- B

n =- N n = N

*******

Итак, рассмотрим случай 5.

Случай 5

(16)

(17´)

(18´)

(19).

Тогда сумма имеет вид:

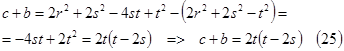
Учитывая (14) и (19), можно получить разность :

=> .

 Скачать реферат