Доказательство утверждения, частным случаем которого является великая теорема Ферма

Выразим из (25) и (26) :

=>

=> .

По условию =35 height=19 src="images/referats/7515/image113.png">должны быть взаимно простыми целыми числами, поэтому их общий множитель .

Т.о., имеют вид:

, , а их сумма .

Т.к. из (8) , то => .

Из (19) с учетом (29) выразим :

, т.е. .

Т.о., , , т.е.

,

выражения которых, с учетом (33), полностью совпадают с (9) и (10).

Теперь, с учетом (17′) и (18´), найдем разность :

т.к. , т.е. (36´).

(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (29). В последующих действиях мы это учтем).

Теперь, учитывая (32), найдем разность (b-n)-n:

где .

Т.к. b + c =2n, то b-2n = b - (b + c) = - c = -1 => c= 1 (40).

Учитывая (34), получим => (38´).

Теперь, с учетом (38´), можно получить окончательное выражение для b (из (35)):

, т.е.(41).

Таким образом, уравнение (15), решениями которого являются (16), (17′), (18´) и (19), в конечном счете, имеет следующие решения:

(41), , где - взаимно простые нечетные целые (40),(38´), числа

*******

Случай 6

Нетрудно догадаться, что если бы у уравнения (15) были бы решения, противоположные по знаку с решениями (16), (17′), (18´) и (19), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (40), (41), (38´´) и (33), т.е.

(40´),(38),

(41´), (33´), где - взаимно простые целые нечетные числа.

*******

Случай7

(16)

(17´)

(18´)

(19´)

Тогда сумма имеет вид:

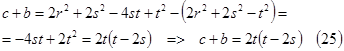
Учитывая (14) и (19´), можно получить разность :

=> (26´).

Выразим из (25) и (26´) :

=>

=> .

По условию должны быть взаимно простыми целыми числами, поэтому их общий множитель .

Т.о., имеют вид:

(30´), (31´), а их сумма .

Т.к. из (8) , то => .

Из (19´), с учетом (29), выразим :

, т.е. (33´).

Т.о., , , т.е.

(34´),

 Скачать реферат