Методы оптимизации при решении уравнений
Задание №1
Определить, существует ли кривая ![]() , доставляющая функционалу экстремум и, если существует, то найти ее уравнение.
, доставляющая функционалу экстремум и, если существует, то найти ее уравнение.
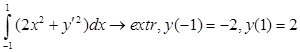
Решение: Составим уравнение Эйлера и найдём его общее решение:
![]()
![]()
Используем краевые условия:
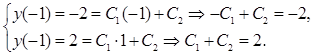
Решаем систему уравнений и получаем:
![]()
Таким образом, экстремаль имеет уравнение вида
![]()
Так как
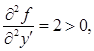
то функционал на прямой ![]() достигает минимума.
достигает минимума.
Задание №2
Найти, используя уравнение Эйлера-Лагранжа, оптимальное управление ![]() , минимизирующее функционал
, минимизирующее функционал ![]() для системы, описываемой уравнениями
для системы, описываемой уравнениями
![]() ,
,
при начальных и конечных условиях соответственно:
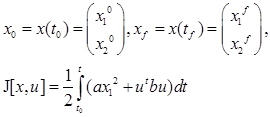
|
A |
B |
t0 |
tf |
x0 |
xf |
a |
b |
|
0 1 0 0 |
0 1 |
0 |
1 |
1 0 |
0 0 |
0 |
1 |
Решение
Формируем задачу по исходным данным:
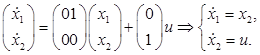 (1)
(1)
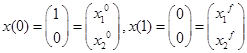 (2)
(2)
![]()
Составим функцию Лагранжа и гамильтониан:
![]()
и соответственно уравнения Эйлера-Лагранжа (здесь для Н):
![]() (3)
(3)
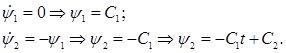 (4)
(4)
Используя замену (3), подставим выражения (4) во второе уравнение динамики в (1):
![]()
![]()
и находим общее решение
![]() (5)
(5)
Подставим его в первое уравнение (1):
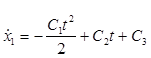
и находим общее решение:
![]() (6)
(6)
Для ![]() из (6) и
из (6) и ![]() из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1, С2, С3, С4,:
из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1, С2, С3, С4,:
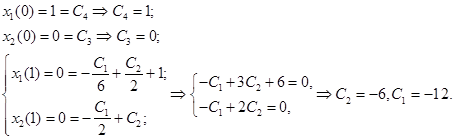
Таким образом, решение имеет вид:
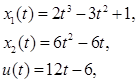
которое удовлетворяет начальным и конечным условиям.
Задание №3
Для системы, описываемой уравнениями
![]()
с заданными условиями на начальное ![]() и конечное
и конечное ![]() значение координат, найти оптимальное управление
значение координат, найти оптимальное управление ![]() , минимизирующее функционал
, минимизирующее функционал
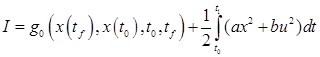
|
A |
B |
t0 |
tf |
x0 |
xf |
g0 |
a |
b |
|
0 1 0 0 |
0 1 |
0 |
t |
1 0 |
x1(tf) = -tf2 |
0 |
0 |
1 |
Решение. Формулируем задачу по исходным данным
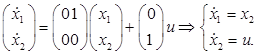 (1)
(1)
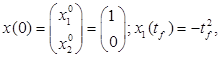 (2)
(2)
т.е. ![]() , подвижна на правом конце, координата
, подвижна на правом конце, координата ![]() - свободна на правом конце,
- свободна на правом конце,
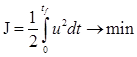
Составим функцию Гамильтона Н (или функцию Лагранжа L)
![]() (3)
(3)
и соответствующие уравнения Эйлера-Лагранжа:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Составим вспомогательную функцию
![]() ,
,
где ![]() . Таким образом:
. Таким образом:
![]() . (7)
. (7)
Поскольку ![]() и
и ![]() подвижны, то используем условия трансверсальности:
подвижны, то используем условия трансверсальности:
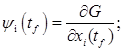
![]() (8)
(8)
![]() (9)
(9)
Так как не фиксирован момент времени ![]() , то используем условие трансверсальности
, то используем условие трансверсальности
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
