Математическое моделирование и расчет систем управления техническими объектами

Изложены основные характеристики систем управления техническими объектами и принципы построения математических моделей таких систем. Рассмотрены разновидности и методы динамического моделирования технологических объектов с позиций исследования их в системах управления. Отмечены особенности построения моделей на базе линейных и нелинейных элементов систем управления.

Пособие предназначено

для студентов всех форм обучения специальности 180400 «Электропривод и автоматика промышленных установок и технологических комплексов» и может быть использовано студентами других специальностей для курсового и дипломного проектирования

Рецензент к.т.н. А.А.Сарвин (Северо-Западный государственный заочный технический ун-т).

Математическое моделирование и расчет систем управления техническими объектами:

Б82 Учебное пособие /Б.М.Борисов, В.Е.Большаков, В.И.Маларёв, Р.М.Проскуряков; Санкт-Петербургский государственный горный институт (технический университет). СПб, 2002. 63 с.

ВВЕДЕНИЕ

Современное горное производство характеризуется достаточным арсеналом средств автоматизации и управления. Для их рационального использования необходимо определить и реализовать оптимальные параметры автоматических систем и регуляторов. Определение оптимальных параметров возможно на стадии проектирования путем изучения поведения моделей управляемых технологических установок, процессов.

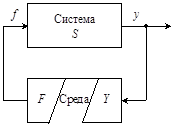
В процессе изучения дисциплины «Математическое моделирование и расчет систем управления техническими объектами» анализируются функциональные схемы управления технологических процессов, определяются взаимосвязи между подсистемами, ограничения, критерии управления. Рассматриваются статические и динамические режимы работы машин, установок и их математическое описание. Изучаются особенности методов исследования математических моделей, имеющих нелинейные зависимости, трансцендентные уравнения.

1. Математические модели систем управления

1.1 Операторы преобразования переменных

Рассмотрение причинно-следственного взаимодействия системы управления со средой связано с обособлением собственно системы S и выделением ее связей со средой через переменные входа f и выхода у (рис.1).

Система оказывается звеном в искусственно разорванной цепи причинно-следственных отношений «среда – система – среда».

На содержательном уровне объекты и системы управления интерпретируются как устройства получения, передачи и обработки информации. С другой стороны, объекты и системы можно рассматривать как преобразователи сигналов – носителей этой информации. Преобразование сводится к изменению параметров, кодирующих информацию. Свойства системы как преобразователя характеризуются ее оператором, отображающим множество функций времени на входе системы на множество функций выхода:

.

Оператор линеен, если обладает свойствами однородности и аддитивности, т. е.

В общем случае линейной комбинации входных воздействий отвечает та же линейная комбинация соответствующих реакций:

Свойство линейности оператора, выраженное приведенной формулой, иногда называют принципом суперпозиции. Принцип суперпозиции дает возможность выражать реакцию линейной системы на любое воздействие через ее реакцию на определенный вид элементарных воздействий fi(t).

При построении моделей стремятся к их простоте при максимальной адекватности оригиналам. В частности, принимают гипотезу о линейности оператора, что принципиально упрощает анализ и синтез.

Если принцип суперпозиции не выполняется, то оператор называется нелинейным. Разумеется, класс нелинейных операторов много богаче класса линейных.

Оператор стационарен, если его характеристики инвариантны ко времени. Другими словами, при сдвиге во времени входного воздействия без изменения его формы реакция претерпевает такой же сдвиг во времени без изменения своей формы. В ряде случаев модели должны отражать изменение свойств объекта во времени, тогда вводятся в рассмотрение нестационарные операторы

Нестационарность оператора учитывает воздействие среды принципиально иного характера, чем сигнальный вход f(t). В простейшем случае нестационарность сводится к изменению параметров модели, например коэффициентов дифференциального уравнения. В общем случае влияние среды приводит к необходимости изменения структуры оператора, например порядка дифференциального уравнения.

Если вариации оператора происходят много медленнее основных процессов, то вместо нестационарного оператора рассматривают множество стационарных операторов, различающихся значениями параметров. Описание объекта множеством равновероятных операторов содержит неопределенность. Если параметры модели заданы с точностью до интервалов значений, то о таких системах говорят, что они интервальные.

Оператор может быть детерминированным или стохастичным. В случае стохастичных операторов параметры представляются как случайные величины и задаются их вероятностные характеристики.

Объекты управления могут быть с сосредоточенными или распределенными параметрами. В последнем случае они описываются уравнениями в частных производных (разностях).

1.2 Классы моделей

Модель объекта или системы управления принадлежит тому же классу, что и описывающий их оператор преобразования. Выделяют следующие признаки классов систем с непрерывным и дискретным временем:

• линейные Л или нелинейные Л;

• стационарные С или нестационарные С;

• детерминированные Д или стохастичные Д;

• сосредоточенные (конечномерные) К или распределенные (бесконечномерные) К.

Эти четыре независимых признака биальтернативны, поэтому можно насчитать всего 24 = 16 классов непрерывных и столько же дискретных систем.

Простейший класс – ЛСДК – линейные стационарные детерминированные конечномерные системы. Они имеют форму обыкновенных линейных дифференциальных (разностных) уравнений с постоянными детерминированными коэффициентами. Математика разработала весьма развитый аппарат анализа этого класса систем.

Более сложные классы операторов получаются при введении одного из альтернативных признаков:

ЛСДК; ЛСДК; ЛСДК; ЛСДК.

Для таких систем существует незначительное число общих методов аналитического исследования, разработанных только для частных случаев. Операторы второго уровня сложности получаются введением двух отрицаний:

ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК; ЛСДК.

При трех отрицаниях получаем операторы третьего уровня сложности:

 Скачать реферат