Математическое моделирование и расчет систем управления техническими объектами

где f – Р-мерный вектор входа;у – K-мерный вектор выхода; A – матрица состояний; B – матрица входа; C – матрица выхода; D – матрица обхода соответствующих размеров. Первую векторно-матричную строку в системе уравнений (18) называют уравнениями состояний, а вторую – уравнениями выхода.

Пример. При n = 2 дифференциальные уравнения (18) системы с одним входом и одни

м выходом в раскрытой форме запишутся так:

Матрицы будут иметь следующий вид:

A = ; B = ;

C = (c1 c2); D = d.

Если первое уравнение в системе (18) записать с использованием оператора дифференцирования р, то имеем: (pI – A)n = Bf, где I – единичная матрица. Таким образом, уравнения в форме пространства состояний являются частным случаем системы дифференциальных уравнений (17) с матрицей

A(p) = pI – A. (19)

Автономная система описывается однородным дифференциальным уравнением

; ,

причем начальные условия являются математическим отражением предыстории. Если они ненулевые, то система совершает так называемые свободные движения. В конечномерных системах свободные движения определяются полностью оператором А(р) и конечным числом начальных условий независимо от того, каким путем система пришла в это состояние к моменту начала наблюдения.

Автономная система может описываться системой дифференциальных уравнений различных порядков:

A(p)x(t) = 0, x(0);

y(t) = Cx(t),

а также дифференциальными уравнениями в форме пространства состояний

= An, n(0);

y = Cn.

Рассмотрим построение моделей вход-выход по системе дифференциальных уравнений. Пусть дана система дифференциальных уравнений (17). Построение модели в терминах «вход-выход» означает исключение внутренних переменных, что проще выполнить, если от дифференциальных уравнений перейти к системе алгебраических уравнений для изображений, приняв нулевые начальные условия:

A(s)X(s) = B(s)F(s); (20)

Y(s) = CX(s).

При небольшом числе уравнений применяют метод последовательных исключений. Пусть, например, объект с одним входом f и одним выходом у имеет две внутренние переменные x1 и х2:

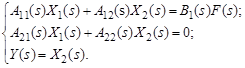(21)

Решая систему (21) относительно Y(s), получим:

Теперь по выражению

легко получить полиномы числителя и знаменателя передаточной функции и записать выражение для одного дифференциального уравнения. Используем операции перемножения и вычитания полиномов.

В случае, когда требуется вычислить передаточную функцию, связывающую одну из выходных переменных у = xq с одним из воздействий fr, применяют правило Крамера:

, (22)

где полиномиальная матрица Aqr получена из матрицы А заменой q-го столбца r-м столбцом матрицы В. Знаменатель передаточной функции Wqr(s) независимо от номеров входа r и выхода q равен характеристическому полиному системы

A(s) = det A(s) (23)

Этот способ построения моделей вход-выход по системе уравнений (20) сводится к вычислению определителей полиномиальных матриц.

Для примера (21) запишем систему в матричной форме (20); матрицы имеют вид:

A(s) = ; B(s) = . (24)

В соответствии с правилом Крамера по формуле (23) определяем характеристический полином:

числитель передаточной функции W21(s) (здесь r = 1, q = 2) равен

det A21 =

Имеем систему алгебраических уравнений многомерной системы, записанную для изображений переменных (20). В общем случае передаточная матрица системы, т.е. модель вход-выход через полиномиальные матрицы выражается следующим образом:

W(s) = CA-1(s)B(s). (25)

Здесь вычисления связаны с обращением и перемножением полиномиальных матриц. Ясно, что полиномиальная матрица системы А(s) должна быть не особенной, иными словами, ее определитель не равен тождественно нулю. Известно, что

,

где А*(s) – присоединенная матрица.

Следовательно, выражение для передаточной матрицы (25) примет вид:

W(s) = CA*(s)B(s)/A(s). (26)

Пример. Модель вход-выход в виде линейного дифференциального уравнения

y(n) + a1y(n-1) + … + an-1y(1) + any = b0u(n) + b1u(n-1) + … + bnu

может быть приведена к модели в переменных состояния следующим образом:

x(1) = xi + 1 + ki*u, где i = 1, n-1;

x(1)n = – anx1 – an-1x2 –…– a1xn + knu;

y = x1 + k0u;

коэффициенты k рассчитываются по рекуррентным формулам:

k0 = b0;

k1 = b1 – a1k0;

…

;

,

где n = 3; a1 = 0; a2 = 2; a3 = 4; b0 = 2; b1 = b2 = 0; b3 = –1.

Определим значение ki:

k0 = b0 = 2;

k1 = b1 – a1*k0 = 0;

k2 = b2 – a1k1 – a2k0 = – 4;

k3 = b3 – a1k2 – a2*k1 – a3k0 = – 9.

Тогда исходное уравнение в переменных состояниях (нормальная форма):

x1(1) = x2;

x2(1) = x3 – 4u;

x3(1) = – 4x1 – 2x2 – 9u;

y = x1 + 2u,

или в векторной форме

;

,

где матрицы объекта, управления, наблюдения и обхода, соответственно,

; ; ; .

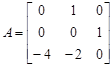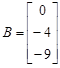2.5 Построение моделей вход-выход по уравнениям в форме пространства состояний

Пусть дифференциальные уравнения объекта или системы управления записаны в форме пространства состояний:

An + Bf, n(0);

(27)

y = Cn + df.

Для простоты примем одномерный случай: переменные входа и выхода f и y являются скалярами; матрица входа В – столбец; матрица выхода С – строка; d – скаляр обхода.

 Скачать реферат