Структурные особенности учебного материала в школьном курсе тригонометрии

, т.к. – прямоугольник

или

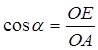, "images/referats/11760/image311.png">

Скалярное произведение

. Т.д.

Из теоремы 1.1 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно:

Если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.

Продолжение п. 6.1 Формулы сложения тригонометрических функций

Повторив весь нужный материал для доказательства формулы косинуса разности приступим к доказательству.

Доказательство.

Мы остановились на рисунке 1, теперь найдем скалярное произведение векторов и . Пусть координаты т. равны и , координаты т. равны и . Эти же координаты имеют соответственно и векторы и . По определению скалярного произведения векторов:

=+.

Выразим скалярное произведение через тригонометрические функции углов и . Из определения косинуса и синуса следует, что

, , , .

Подставив значения ,,, в правую часть равенства =+, получим

==

.

Значит

С другой стороны, по теореме о скалярном произведении векторов имеем

=

Угол между векторами и может быть равен (рис.7), (рис.8) либо может отличаться от этих значений на целое число оборотов.

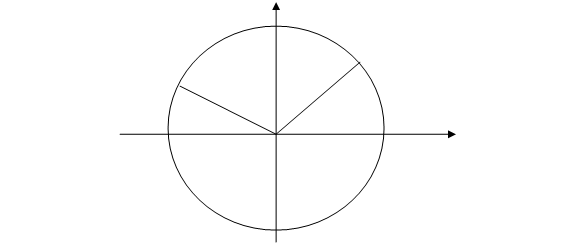
Рис.7

Рис.8

В любом из этих случаев

Поэтому

Т.к. равно также , то

= (1)

Формулу (1) называют формулой косинуса разности. Косинус разности двух углов равен произведению этих углов плюс произведение синусов этих углов.

С помощью формулы (1) можно легко получить формулу косинуса суммы

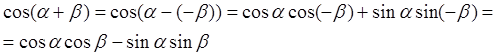
(, т.к. косинус является четной функцией, , т.к. синус является нечетной функцией).

Значит, (2)

Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.

Выведем теперь формулы синуса суммы и синуса разности.

Используя формулы приведения (которые нами уже были рассмотрены) и формулу (1), получим

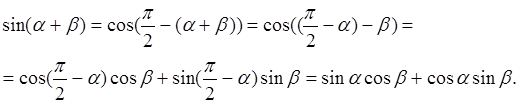
Значит, (3)

Синус суммы двух улов равен произведению синуса первого угла на косинус второго плюс произведение косинуса первого угла на синус второго.

Для синуса разности имеем:

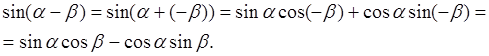
Значит, (4)

Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение косинуса первого угла на синус второго.

 Скачать реферат