Структурные особенности учебного материала в школьном курсе тригонометрии
Длиной (абсолютной величиной или модулем) ненулевого вектора ![]() называется длина отрезка
называется длина отрезка ![]() . Длина вектора
. Длина вектора ![]() (вектора
(вектора ![]() ) обозначается так: |
) обозначается так: |width=27 height=23 src="images/referats/11760/image269.png">| (|
![]() |). Длина нулевого вектора считается равной нулю: |
|). Длина нулевого вектора считается равной нулю: |![]() |=0.
|=0.
6.3 Основные свойства векторов
Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос (определение и свойства параллельного переноса в этом же 8 классе на стр. 145), который переводит начало и конец одного вектора в начало и конец другого вектора.
Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине.
Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.
Пусть вектор ![]() имеет началом точку
имеет началом точку ![]() , а концом –
, а концом – ![]() . Координатами вектора
. Координатами вектора ![]() будем называть числа
будем называть числа ![]() ,
, ![]() . Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае
. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае ![]() или просто
или просто ![]() . Координаты нулевого вектора равны нулю.
. Координаты нулевого вектора равны нулю.
Из формулы
![]()
где ![]() – расстояние между точками
– расстояние между точками ![]() и
и ![]() , следует, что абсолютная величина вектора
, следует, что абсолютная величина вектора ![]() с координатами
с координатами ![]() равна
равна ![]() .
.
Равные векторы имеют равные соответствующие координаты. И обратно:
Если у векторов соответствующие координаты равны, то векторы равны.
Произведением вектора ![]() на число
на число ![]() называется вектор
называется вектор
![]() , т.е.
, т.е. ![]() .
.
По определению ![]() .
.
Скалярным определением векторов ![]() и
и ![]() называется число
называется число ![]() .
.
Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение ![]() обозначается
обозначается ![]() и называется скалярным квадратом. Очевидно,
и называется скалярным квадратом. Очевидно, ![]() .
.
Из определения скалярного определения векторов следует, что для любых векторов
![]() ,
, ![]() и
и ![]()
![]() .
.
Действительно, левая часть равенства есть
![]() , а правая
, а правая ![]()
Очевидно, что они равны.
Углом между векторами ![]() и
и ![]() называется угол
называется угол ![]() . Углом между любыми двумя ненулевыми векторами
. Углом между любыми двумя ненулевыми векторами ![]() и
и ![]() называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю.
называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю.
Теорема 1.1.
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство.
Пусть ![]() и
и ![]() – данные векторы и
– данные векторы и ![]() – угол между ними. Имеем
– угол между ними. Имеем
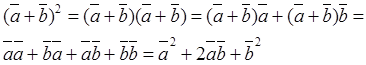
или ![]()
Отсюда видно, что скалярное произведение ![]()
![]() выражается через длины векторов
выражается через длины векторов ![]() ,
, ![]() и
и ![]() +
+![]() , а поэтому зависит от выбора системы координат, т.е. скалярное произведение не изменится, если систему координат выбрать специальным образом. Возьмем систему координат
, а поэтому зависит от выбора системы координат, т.е. скалярное произведение не изменится, если систему координат выбрать специальным образом. Возьмем систему координат ![]() так, как показано на рис.6.
так, как показано на рис.6.
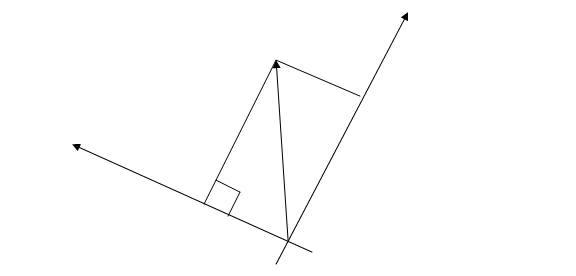
Рис.6
При таком выборе системы координат координатами вектора ![]() будут
будут ![]() и
и ![]() , а координатами вектора
, а координатами вектора ![]() будут
будут ![]() и
и ![]() . Это следует из прямоугольного
. Это следует из прямоугольного ![]() :
: ![]() , т.к.
, т.к. ![]()
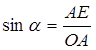 ,
, ![]()
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
