Интеграл Лебега-Стилтьеса
Введение
Понятие интеграла Римана, известное из элементарного курса анализа, применимо лишь к таким функциям, которые или непрерывны или имеют "не слишком много" точек разрыва. Для измеримых функций, которые могут быть разрывны всюду, где они определены (или же вообще могут быть заданы на абстрактном множестве, так что для них понятие непрерывности просто не имеет смысла)
, римановская конструкция интеграла становится непригодной. Вместе с тем для таких функций имеются аналоги в теории измерений: это интегралы Лебега и Стилтьеса. Так как интеграл Стилтьеса охватывает более широкий класс функций, мы остановимся на рассмотрении этого интеграла.
Выбор темы обусловлен тем, что изучению интеграла Стилтьеса уделяется меньше внимания, чем интегралам Римана и Лебега, хотя именно идея стилтьесовского интегрирования богаче и плодотворней предыдущих, определение интеграла Стилтьеса шире классического и в некотором отношении удобнее его.
Цель работы - рассмотреть необходимость введения понятия интеграла Стилтьеса, дать точное, компактное, сравнительно полное изложение теории интеграла Стилтьеса.
Задачи, которые нужно выполнить для достижения цели:
изучить множество литературы по этой теме;
отобрать из изученного материла необходимый;
привести примеры использования интеграла.
Работа состоит из трёх глав. Первая посвящена развитию данного понятия, проблеме моментов, которая и привела к необходимости введения нового понятия интеграла.
Во второй главе рассмотрены основные понятия, определение самого интеграла, свойства, способы вычисления, рассмотрено множество примеров.
Третья глава посвящена применению интеграла Стилтьеса в других разделах математики и в других науках.
Глава I. Развитие понятия интеграла
1.1 Проблема моментов
Введение понятия интеграла Стилтьеса и последующая его разработка связаны с проблемой моментов, состоящей в следующем. Пусть задана последовательность чисел ![]() ; требуется найти такую функцию распределения
; требуется найти такую функцию распределения ![]() , чтобы члены заданной последовательности были моментами, т.е.
, чтобы члены заданной последовательности были моментами, т.е. 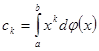 . Если a и b конечны, то поставленная задача называется проблемой моментов в конечном интервале; если
. Если a и b конечны, то поставленная задача называется проблемой моментов в конечном интервале; если ![]() , то получаем проблему моментов Стилтьеса.
, то получаем проблему моментов Стилтьеса.
Проблема моментов первоначально ставилась в менее общей форме. А именно по заданной последовательности чисел ![]() ищется такая функция
ищется такая функция ![]() , чтобы имели место равенства
, чтобы имели место равенства 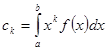 . Целесообразность привлечения интеграла Стилтьеса для постановки и решения проблемы моментов напрашивается довольно естественно. С таким положением вещей и столкнулся Стилтьес при изучении непрерывных дробей, и именно в результате этих исследований он предложил своё обобщение интеграла.
. Целесообразность привлечения интеграла Стилтьеса для постановки и решения проблемы моментов напрашивается довольно естественно. С таким положением вещей и столкнулся Стилтьес при изучении непрерывных дробей, и именно в результате этих исследований он предложил своё обобщение интеграла.
Ранние исследования Стилтьеса изложены в его статье о механических квадратурах, в которой выясняется, позволяют ли формулы квадратур получать неограниченное приближение интеграла в смысле Римана. Во вводной части статьи Стилтьес решает задачу об определении многочлена
![]()
Условиями
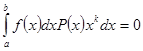
![]() (1)
(1)
при неотрицательной ![]() на
на ![]() .
.
Мы коснемся двух моментов из содержания его статьи.
Первый относится к задаче о степени приближения, даваемого квадратурной формулой Гаусса:
![]()
![]()
Здесь Стилтьес пользуется доказанными им формулами П.Л. Чебышева в виде
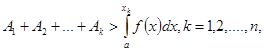
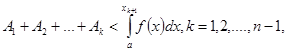
где ![]() . (2)
. (2)
Он показывает, что если в квадратурной формуле Гаусса в качестве ![]() брать числа
брать числа ![]() , получаемые по формуле (2) из цепной дроби, соответствующей интегралу
, получаемые по формуле (2) из цепной дроби, соответствующей интегралу ![]() , а
, а ![]() будут корнями знаменателей подходящих дробей, то формула Гаусса даст сколь угодно точное приближение при возрастании
будут корнями знаменателей подходящих дробей, то формула Гаусса даст сколь угодно точное приближение при возрастании ![]() . Для этой цепной дроби числа
. Для этой цепной дроби числа ![]() , очевидно, удовлетворяют неравенствам
, очевидно, удовлетворяют неравенствам
![]()
![]() (3)
(3)
так как в этом случае ![]() .
.
Вторым моментом является следующий. Отметив, что его результаты полезны при изучении вопроса о квадратуре интеграла 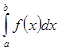 , Стилтьес ставит вопрос о квадратурных формулах для интеграла вида
, Стилтьес ставит вопрос о квадратурных формулах для интеграла вида
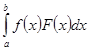 . (4)
. (4)
Он ограничивается тем частным случаем, когда ![]() - произвольная интегрируемая по Риману функция, а
- произвольная интегрируемая по Риману функция, а ![]() такова, что внутри
такова, что внутри ![]() не существует интервала
не существует интервала ![]() , в котором
, в котором 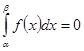 , и показывает, что в этом случае аппроксимация возможна со сколь угодно большой степенью точности. Доказательство этого факта опирается на то, что функция
, и показывает, что в этом случае аппроксимация возможна со сколь угодно большой степенью точности. Доказательство этого факта опирается на то, что функция
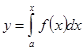 (5)
(5)
является непрерывной и строго монотонной, а потому существует обратная функция ![]() , и в интеграле (4) возможна замена переменных
, и в интеграле (4) возможна замена переменных
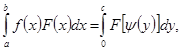
сводящих интеграл (4) к уже изученному Стилтьесом случаю.
По поводу же общего случая Стилтьес указал, что "условия, налагаемые на функции ![]() , делаются источником трудностей, которых удастся избежать лишь с помощью новых исследований о самих принципах интегрального исчисления". Действительно, если
, делаются источником трудностей, которых удастся избежать лишь с помощью новых исследований о самих принципах интегрального исчисления". Действительно, если ![]() не удовлетворяет условию отсутствия в
не удовлетворяет условию отсутствия в ![]() интервала
интервала ![]() , в котором
, в котором 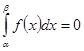 , то она может оказаться не монотонной, поэтому обращение
, то она может оказаться не монотонной, поэтому обращение ![]() в том виде, в каком такую замену тогда производили, становится невозможным, и квадратуру интеграла (4) уже нельзя свести к квадратуре интеграла
в том виде, в каком такую замену тогда производили, становится невозможным, и квадратуру интеграла (4) уже нельзя свести к квадратуре интеграла 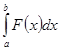 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
