Функция многих переменных

(7.5)

где - неизвестные функции х. Находя производную

и подставляя значение у и у’ в уравнение (7.5), получим

(7.6)

Выберем функцию так, чтобы выражение в скобках равнялось нулю. Для этого надо решить уравнение с разделяющимися переменными.

Решая его, находим

. (7.7)

Постоянную интегрирования в выражении (7.7) не пишем, поскольку нам достаточно найти только какую-нибудь одну функцию , которая преобразовывает в ноль выражение в скобках в уравнении (7.6).

Подставляя (7.7) в (7.6), получим

(7.8)

Подставляя (7.7) и (7.8) в (7.5), найдём общее решение уравнения (7.4):

(7.9)

Замечание. На практике помнить формулу (7.9) не обязательно: достаточно лишь помнить, что линейные дифференциальные уравнения первого порядка, а также уравнения Бернулли, решаются методом Бернулли с помощью подстановки .

Уравнением Бернулли называется уравнение вида

где - известные функции х, .

2. Комплексным числом называется выражение

, (7.10)

где х, у – действительные числа, а символ i – мнимая единица, которая определяется условием . При этом число х называется действительной частью комплексного числа z и обозначается , а у – мнимой частью z и обозначается (от французских слов: reel – действительный, imaginare – мнимый). Выражение (7.10) называется алгебраической формой комплексного числа.

Два комплексных числа и , которые отличаются только знаком мнимой части, называются сопряжёнными.

Два комплексных числа и считаются равными тогда и только тогда, когда равны их действительные и мнимые части:

Комплексные числа можно изображать на плоскости. Так число (7.10) изображается в прямоугольной системе координат точкой М(х;у). Такая плоскость называется комплексной плоскостью переменной z, ось Ох называется действительной, у

а ось Оу – мнимой.

При у=0 комплексное число является одновременно

у М(х;у)

действительным числом. Поэтому действительные числа являются

отдельным случаем комплексных, они изображаются на оси Ох.

Комплексные числа , в которых х=0, называются чисто

мнимыми; такие числа изображаются на оси Оу.

0 х х

Полярные координаты точки М(х;у) на комплексной плоскости называются модулем и аргументом комплексного числа и обозначаются

Поскольку , то по формуле (7.10) имеем

.

Это выражение называется тригонометрической формой комплексного числа z.

Модуль комплексного числа определяется однозначно, а аргумент – с точностью до 2:

.

Здесь - общее значение аргумента, а - главное значение аргумента, которое находится на промежутке [0;и отсчитывается от оси Ох против часовой стрелки.

Если , то считают, что а - неопределён.

Арифметические действия над комплексными числами, заданными в алгебраической форме, выполняются по обычным правилам действий над двучленами с учётом того, что . Так, если

, , то

1)

2)

3)

4) .

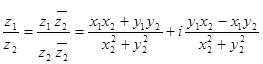Рассмотрим действия над комплексными числами в тригонометрической форме.

Пусть

, .

Тогда

=

Значит, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на произвольное конечное число множителей. В частности,

 Скачать реферат