Функция многих переменных

0 а х![]() х
х![]()
![]() х
х![]() b x
b x
Разобьём отрезок [a;b] произвольным образом на п частей
точками а=х![]() <x
<x![]() <…< х
<…< х![]() < х
< х![]() <… <х
<… <х![]() =b.
=b.
На каждом отрезке [х![]() ; х
; х![]() ] возьмём произвольную точку
] возьмём произвольную точку ![]() и вычислим значение f(
и вычислим значение f(![]() ). Тогда площадь S
). Тогда площадь S![]() заштрихованного прямоугольника, будет равна
заштрихованного прямоугольника, будет равна
S![]() = f(
= f(![]() )
)![]() , где
, где ![]() = х
= х![]() - х
- х![]() .
.
Площадь S всей трапеции приблизительно равна
S![]()
![]() .
.
Пусть ![]() . Естественно считать, что
. Естественно считать, что
S![]() . (6.2)
. (6.2)
К пределам вида (6.2) приводят много других задач, поэтому возникает необходимость всестороннего изучения таких пределов независимо от конкретного содержания той или иной задачи.
Пусть функция у= f(x) определена на отрезке [a;b]. Разобьём этот отрезок на п произвольных частей точками
а=х![]() <x
<x![]() <…< х
<…< х![]() < х
< х![]() <… <х
<… <х![]() =b.
=b.
На каждом из созданных отрезков [х![]() ; х
; х![]() ] возьмём произвольную точку
] возьмём произвольную точку ![]() и составим сумму
и составим сумму
![]() , где
, где ![]() = х
= х![]() - х
- х![]() ,
,
которую будем называть интегральной суммой функции f(x).
Обозначим ![]() . Если существует конечный предел интегральной суммы
. Если существует конечный предел интегральной суммы ![]() , при
, при ![]() , который не зависит ни от способа разбиения отрезка [a;b], ни от выбора точек
, который не зависит ни от способа разбиения отрезка [a;b], ни от выбора точек![]() , то этот предел называется определённым интегралом функции f(x) на отрезке [a;b] и обозначается символом
, то этот предел называется определённым интегралом функции f(x) на отрезке [a;b] и обозначается символом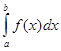 , где функция f(x) называется интегрированной на отрезке [a;b].
, где функция f(x) называется интегрированной на отрезке [a;b].
То есть, по определению,
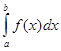 =
=![]() .
.
Числа а и b называются соответственно нижним и верхним пределом интегрирования.
Относительно существования определённого интеграла имеет место такая теорема
Теорема 6.3. Если функция f(x) ограничена на отрезке [a;b] и непрерывна на нём везде, кроме конечного числа точек, то она интегрируема на этом отрезке.
2. Если f(x)![]() , то
, то 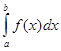 равен площади соответствующей криволинейной трапеции:
равен площади соответствующей криволинейной трапеции: 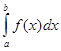 =S. Если f(x)<0, то
=S. Если f(x)<0, то 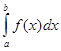 = -S.
= -S.
Отсюда следует, что если на симметричном относительно начала координат отрезке [-a;а], а>0 задана нечётная функция, то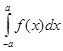 =0. Например,
=0. Например, ![]() Если функция f(x) чётная, то
Если функция f(x) чётная, то 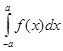 =2
=2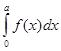 .
.
Свойства определённого интеграла
Будем считать, что все интегралы, которые рассматриваются, существуют.
1. 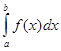 =
=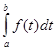 . Величина определённого интеграла не зависит от обозначения переменной интегрирования.
. Величина определённого интеграла не зависит от обозначения переменной интегрирования.
2. 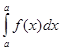 =0.
=0.
3. 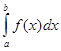 = -
= -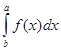 .
.
4. 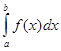 =
=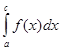 +
+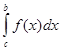 .
.
5. 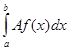 =А
=А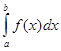 .
.
6. 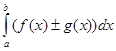 =
=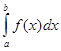
![]()
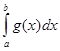 .
.
7. Если на отрезке [a;b] f(x)![]() , то
, то 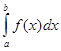
![]()
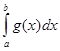 .
.
8. Если т и М – соответственно наименьшее и наибольшее значения функции f(x), на отрезке [a;b], то
т(b-a) ![]()
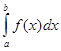
![]() M(a-b).
M(a-b).
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
