Функция многих переменных

Символически это можно записать так:

d2 z=(dх+dу)2 z.

Аналогично можно получить формулу для полного дифференциала п-го порядка:

dп z= d(dп-1 z) =(dх+ight=44 src="images/referats/7449/image054.png">dу)п z.

2. Производная функции z=f(x;у) в направлении вектора вычисляется по формуле

+,

где , - направляющие косинусы вектора :

= , = .

Если частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей, то производная в направлении вектора определяет скорость изменения функции в направлении вектора .

Градиентом функции z=f(x;у) называется вектор

grad z=(,).

Свойства градиента

1. Производная имеет наибольшее значение, если направление вектора совпадает с направлением градиента, причём это наибольшее значение производной равно .

2. Производная в направлении вектора, перпендикулярного градиенту, равна нулю.

3. Пусть функция z=f(x;у) определена на множестве D и точка М(х;у)D. Если существует окрестность точки М, которая принадлежит множеству D, и для всех отличных от Мточек М выполняется неравенство

f(М)< f(М0) (f(М)> f(М0)),

то точку Мназывают точкой локального максимума (минимума) функции z=f(x;у), а число f(М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.

Теорема 5.1 (необходимые условия экстремума). Если функция z=f(x;у) в точке М( х;у) имеет локальный экстремум, то в этой точке частные производные ,равны нулю или не существуют.

Точки, в которых == 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.

Поэтому функция может достигать экстремальных значений только в критических точках; однако не всякая критическая точка является точкой экстремума.

Пусть в стационарной точке М( х;у) и некоторой её окрестности функция z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:

А=( х;у), В=( х;у), С=( х;у), =АС-В2.

Теорема 5.2 (достаточные условия экстремума).

1. Если >0, то функция z=f(x;у) в точке Мимеет экстремум, причём максимум при А<0 и минимум при А>0.

2. Если <0, то в точке Мнет экстремума.

Для случая, когда количество переменных п>2, пользуются такой теоремой.

Теорема 5.3 Функция и= f(х; .;х) имеет минимум в стационарной точке М, если дифференциал второго порядка этой функции в точке Мположителен d2f(М)>0, и максимум, если d2f(М)<0.

Пример. Исследовать на экстремум функцию

z=(х+2)2+(у -1)2.

Решение.

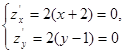
Функция имеет одну критическую точку М(-2;1).

 Скачать реферат