Математический анализ. Практикум

Точки, в которых частные производные обращаются в нуль или не существуют, называются критическими.

Достаточный признак экстремума. Пусть функция определена в некоторой окрестности критической точки и имеет в этой точке непрерывные частные производные второго порядк

а

Тогда

1) имеет локальный максимум в точке , если и ;

2) имеет локальный минимум в точке , если и ;

3) не имеет локального экстремума в точке , если ;

Схема исследования на экстремум функции двух переменных.

1. Найти частные производные функции :и .

2. Решить систему уравнений , и найти критические точки функции.

3. Найти частные производные второго порядка, вычислить их значения в критических точках и с помощью достаточного условия сделать вывод о наличии экстремумов.

4. Найти экстремумы функции.

Пример 51. Найти экстремумы функции .

Решение.

1) Найдем частные производные .

2) Решим систему уравнений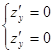

3)

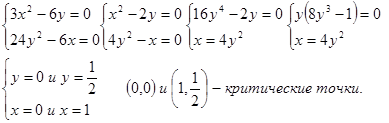
4) Найдем частные производные второго порядка и их значения в критических точках: . В точке получим:

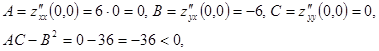
значит, в точке экстремума нет. В точке получим:

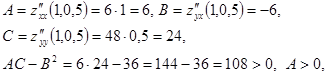
значит, в точке минимум.

5) .

Ответ.

5.2 Глобальный экстремум (наибольшее и наименьшее значение функции)

Наибольшее и наименьшее значения функции нескольких переменных, непрерывной на некотором замкнутом множестве, достигаются или в точках экстремума, или на границе множества.

Схема нахождения наибольшего и наименьшего значений.

1) Найти критические точки, лежащие внутри области, вычислить значение функции в этих точках.

2) Исследовать функцию на границе области; если граница состоит из нескольких различных линий, то исследование необходимо провести для каждого участка отдельно.

3) Сравнить полученные значения функции и выбрать наибольшее и наименьшее.

Пример 52. Найти наибольшее и наименьшее значения функции в прямоугольнике .

Решение. 1) Найдем критические точки функции, для этого найдем частные производные: , и решим систему уравнений:

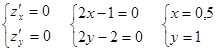
Получили критическую точку A. Полученная точка лежит внутри заданной области,

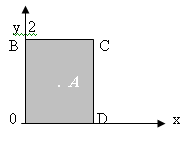
Границу области составляют четыре отрезка: и. найдем наибольшее и наименьшее значение функции на каждом отрезке.

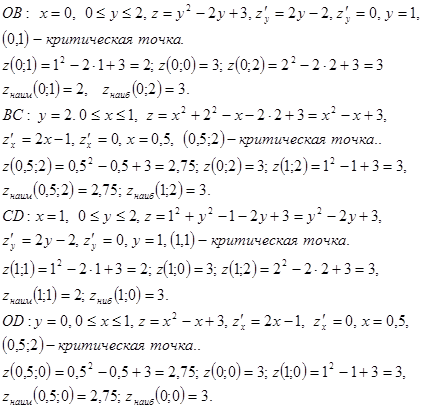
4) Сравним полученные результаты и получим, что в точках .

Глава 6. Модель потребительского выбора

Будем полагать, что имеется n различных товаров. Тогда некоторый набор товаров будем обозначать через n-мерный вектор , где – количество i-того товара. Множество всех наборов товаров X называется пространством.

Выбор индивида-потребителя характеризуется отношением предпочтения: считается, что потребитель может сказать о любых двух наборах, какой более желателен, или он не видит между ними разницы. Отношение предпочтения транзитивно: если набор предпочтительнее набора , а набор предпочтительнее набора , то набор предпочтительнее набора . Будем полагать, что поведение потребителя полностью описывается аксиомой индивида-потребителя: каждый индивид-потребитель принимает решение о потреблении, покупках и т.п., исходя из своей системы предпочтений.

6.1 Функция полезности

На множестве потребительских наборов X определена функция , значение которой на потребительском наборе равно потребительской оценке индивида для этого набора. Функция называется функцией полезности потребителя или функцией потребительского предпочтения. Т.е. каждый потребитель имеет свою функцию полезности. Но все множество потребителей можно разделить на определенные классы потребителей (по возрасту, имущественному положению и т.п.) и каждому классу приписать некоторую, может быть, осредненную функцию полезности.

 Скачать реферат