Математический анализ. Практикум

предел зависит от k, т.е. он в данной точке не существует, а значит, функция имеет в этой точке разрыв.

4.3 Производные и дифференциалы функций нескольких переменных

4.3.1 Частные производные первого порядка

Частная производная функции по аргументу x является обыкновенной производной функции одной переменн

ой x при фиксированном значении переменной y и обозначается:

Частная производная функции по аргументу y является обыкновенной производной функции одной переменной y при фиксированном значении переменной x и обозначается:

Пример 43. Найти частные производные функций.

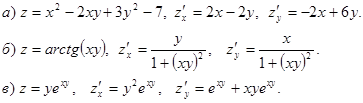
4.3.2 Частные производные второго порядка

Частные производные второго порядка – это частные производные от частных производных первого порядка. Для функции двух переменных вида возможны четыре вида частных производных второго порядка:

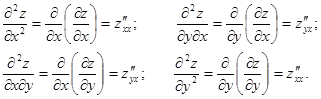
Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называют смешанными производными. Смешанные производные второго порядка дважды дифференцируемой функции равны.

Пример 44. Найти частные производные второго порядка.

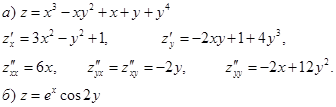
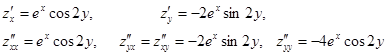
4.3.3 Полный дифференциал и его применение к приближенным вычислениям.

Определение. Дифференциал первого порядка функции двух переменных находится по формуле

.

Пример 45. Найти полный дифференциал для функции .

Решение. Найдем частные производные:

тогда

.

При малых приращениях аргументов x и y функция получает приращение , приблизительно равное dz, т.е. .

Формула для нахождения приближенного значения функции в точке , если известно ее точное значение в точке :

.

Пример 46. Найти .

Решение. Пусть ,

.

Тогда используем формулу

.

Получим:

.

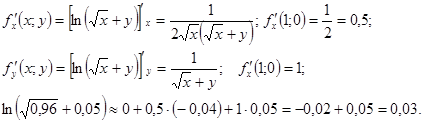
Ответ. .

Пример 47. Вычислить приближенно .

Решение. Рассмотрим функцию . Имеем

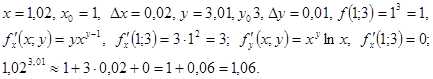
Ответ. .

Пример 48. Вычислить приближенно .

Решение. Рассмотрим функцию . Получим:

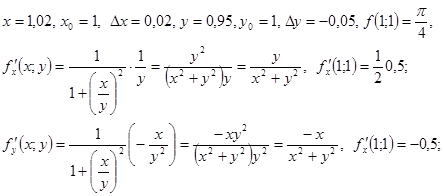
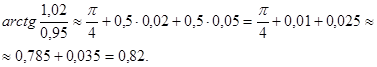
Ответ. .

4.3.4 Дифференцирование неявной функции

Определение. Функция называется неявной, если она задается уравнением , не разрешимым относительно z.

Частные производные такой функции находятся по формулам:

Пример 49. Найти частные производные функции z, заданной уравнением .

Решение.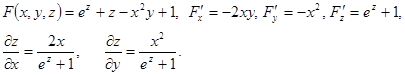

Определение. Функция называется неявной, если она задается уравнением , не разрешимым относительно y.

Производная такой функции находится по формуле:

.

Пример 50. Найти производные данных функций.

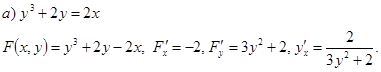
Глава 5. Классические методы оптимизации

5.1 Локальный экстремум функции нескольких переменных

Определение 1. Функция имеет максимум в точке , если для всех точек достаточно близких к точке и отличных от нее.

Определение 2. Функция имеет минимум в точке , если для всех точек достаточно близких к точке и отличных от нее.

Необходимое условие экстремума. Если функция достигает экстремума в точке , то частные производные от функции обращаются в нуль или не существуют в этой точке.

 Скачать реферат