Математический анализ. Практикум

2) Асимптоты.

– вертикальная асимптота, т.к.

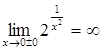
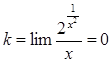– наклонных асимптот нет

, – горизонтальная асимптота

Схематичный график данной функции:

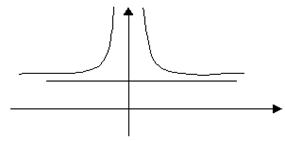
24.

1)

2) Асимптоты

– вертикальная асимптота при , т.к.

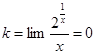– наклонных асимптот нет

, – горизонтальная асимптота

3) – функция убывает на каждом из промежутков.

Схематичный график данной функции:

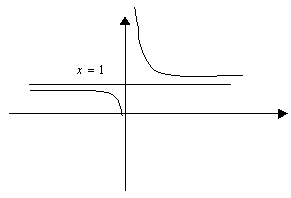
2.4.3 Наибольшее и наименьшее значение функции на отрезке

Чтобы найти наибольшее и наименьшее значение функции на отрезке можно воспользоваться схемой:

1. Найти производную функции .

2. Найти критические точки функции, в которых или не существует.

3. Найти значение функции в критических точках, принадлежащих заданному отрезку и на его концах и выбрать из них наибольшее и наименьшее .

Пример. Найти наименьшее и наибольшее значение функции на данном отрезке.

25. на промежутке

1)

2) – критические точки

3) ,

–

–

26. на промежутке .

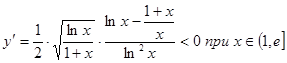
Производная не существует при , но 1 не принадлежит данному промежутку. Функция убывает на промежутке , значит, наибольшего значения нет, а наименьшее значение .

2.5 Правило Лопиталя

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.

Т.е. при раскрытии неопределенностей вида или можно использовать формулу:

.

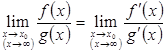Примеры.

27.

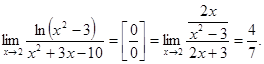
28.

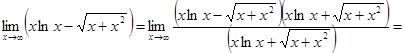
Глава 3. Интегрально исчисление

3.1 Неопределенный интеграл

3.1.1 Определения и свойства

Определение 1. Функция называется первообразной для , если .

Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.

Обозначение: , где c - произвольная постоянная.

Свойства неопределенного интеграла

1. Производная неопределенного интеграла:

2. Дифференциал неопределенного интеграла:

3. Неопределенный интеграл от дифференциала:

4. Неопределенный интеграл от суммы (разности) двух функций:

;

5. Вынесение постоянного множителя за знак неопределенного интеграла:

3.1.2 Таблица интегралов

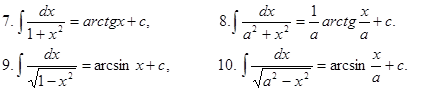
3.1.3 Основные методы интегрирования

1. Использование свойств неопределенного интеграла.

Пример 29.

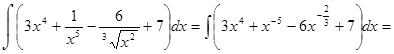
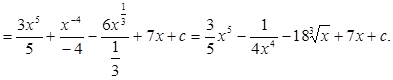
2. Подведение под знак дифференциала.

Пример 30.

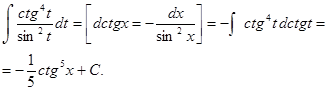
3. Метод замены переменной:

а) замена в интеграле

:

,

где - функция, интегрируемая легче, чем исходная; - функция, обратная функции ; - первообразная функции .

 Скачать реферат