Математический анализ. Практикум

Классификация точек разрыва:

разрыв I рода

- устранимый – односторонние пределы существуют и равны;

- неустранимый (скачок) – односторонние пределы не равны;

разрыв II рода: предел функции в точке не существует.

Пример 16. Установить характер разрыва функции в точке или доказать непрерывность функции в этой точке.

а)

при функция не определена, следовательно, она не непрерывна в этой точке. Т.к. и, соответственно, , то – точка устранимого разрыва первого рода.

б)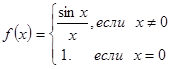

по сравнению с заданием (а) функция доопределена в точке так, что , значит, данная функция непрерывна в данной точке.

в)

При функция не определена;

.

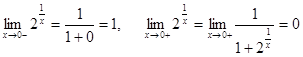Т.к. один из односторонних пределов бесконечен, то – точка разрыва второго рода.

Глава 2. Дифференциальное исчисление

2.1 Определение производной

Определение производной

Производная или от данной функции есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:

или .

Механический смысл производной – скорость изменения функции. Геометрический смысл производной – тангенс угла наклона касательной к графику функции:

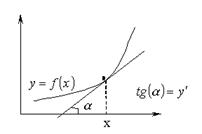
2.2 Основные правила дифференцирования

Производные основных элементарных функций

Пример 17

а)

б)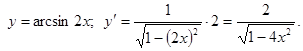

в)

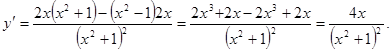
2.3 Производные высших порядков

Производная второго порядка функции

Производная второго порядка функции :

 Скачать реферат