Дифференциальная геометрия торсов в пространстве 1R4 с псевдоевклидовой касательной плоскостью

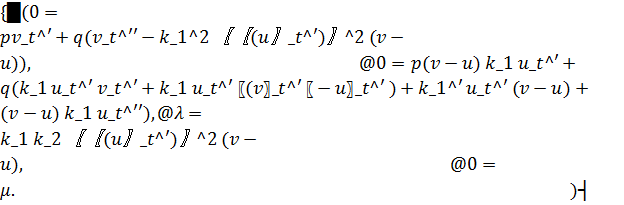
Из системы видим, что если (1,2) – геодезическая линия существует, то она определяется нормалью

. Учитывая этот факт, преобразуем систему следующим образом:

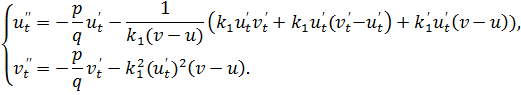
Таким образом, уравнение (1,2) – геодезической линии можно представить в виде нормальной системы дифференциальных уравнений:

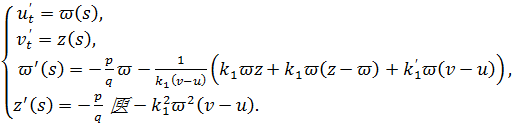(39)

Теорема Пикара. Если правые части системы

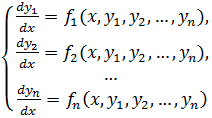
в некоторой окрестности начальной точки () имеют непрерывные в этой окрестности частные производные по , то система имеет единственное решение, определенное в некоторой окрестности точки и удовлетворяющее начальным условиям

.

Согласно теореме Пикара система (39) имеет единственное решение. Значит, через каждую точку торса в каждом направлении касательной плоскости проходит единственная (1,2) – геодезическая линия.

Пусть d: r=r(u(t),v(t)) на торсе является (2,2) – геодезической. Тогда, согласно определению, система (38’) должна быть разрешима при любых коэффициентах и , но т.к. , то это условие не выполняется. Значит, на торсе с касательной псевдоевклидовой плоскостью не существует (2,2) – геодезических линий.

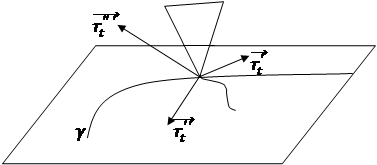
Теорема 5.1. Геодезических линий типа (2,2) на торсе нет.

Рассмотрим вопрос о существовании (1,3) – геодезических линий на торсе. Соприкасающуюся 3-плоскость к кривой в некоторой точке можем задать линейным уравнением

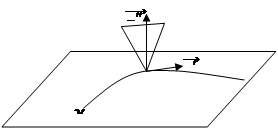
Таким образом, нормальная плоскость и соприкасающаяся 3-плоскость всегда имеют пересечение, являющееся не менее чем прямой. Значит, любая линия на рассматриваемой поверхности является (1,3)-геодезической.

§6. Асимптотические линии на торсе пространства Минковского

Определение 6.1. Направление на поверхности называется асимптотическим, если нормальная кривизна поверхности в этом направлении обращается в нуль.

Определение 6.2. Нормальной кривизной кривой на поверхности пространства Минковского называется проекция вектора кривизны этой кривой на нормальную плоскость к поверхности в этой точке.

Определение 6.3. Кривая на поверхности называется асимптотической линией, если в каждой своей точке она имеет асимптотическое направление.

Определение 6.4. Вектором кривизны кривой на поверхности пространства Минковского будем называть вектор , где s – естественная параметризация на этой кривой.

Пусть - произвольная кривая на торсе. Построим канонический репер кривой в точке N: . Нормальная кривизна кривой в точке N – это проекция вектора кривизны на нормаль к поверхности. В пространстве 1R4 к поверхности в данной точке существует целая плоскость нормалей, поэтому необходимо определить нормаль, на которую будет проецироваться вектор кривизны. Координаты вектора в репере согласно формуле (37) равны:

º(A;B;C;0)

Нормальную кривизну определим как длину отрезка NL1, где L1 – точка пересечения плоскости и проходящей через точку L, с нормальной плоскостью . Определим координаты точки L1:x1=0, x2=0, x3=0, x4=0; Þx3=C, x4=0. Значит, , т.е. нормальная кривизна кривой на торсе пространства Минковского, с псевдоевклидовой касательной плоскостью, является действительной величиной.

Определим геодезическую кривизну кривой как длину отрезка NL2, где L2 – точка пересечения плоскости с касательной плоскостью . Определим координаты точки L2: x3=0, x4=0;x1=0, x2=0; Þx1=A, x2=B. Следовательно, координаты точки L2:

x1=A, x2=B, x3=0, x4=0. |NL2|=.

Рассмотрим нормальную кривизну . Справедлива формула первой квадратичной формы поверхности: , таким образом,

 Скачать реферат