Дифференциальная геометрия торсов в пространстве 1R4 с псевдоевклидовой касательной плоскостью

(24)

В общем случае относительно величин и ничего сказать нельзя. Поэтому будем делать предположение относительно кривой g. Предположим, что касательный вектор к кривой g во всех точках является ве

ктором действительной длины. На ребре возврата g выбираем естественную параметризацию. Пусть u=u(s), тогда и Параметр s обозначим через u, получим , т.е. вектор имеет постоянную длину, тогда поскольку , из (24) следует, что , а значит координатные линии на торсе в такой системе координат не ортогональны. Перейдем к новым координатам U и V так, чтобы координатные линии были ортогональны, причем заметим, чтоv-линии – это прямолинейные образующие торса. При переходе к новым координатам потребуем, чтобы семейство v-линий осталось прежним, а u-линии изменились и стали перпендикулярны v-линиям. Таким образом, перед нами стоит задача отыскания ортогональных траекторий к прямолинейным образующим торса.

Рассмотрим первую квадратичную форму поверхности, которая при условии, что касательная плоскость к торсу является псевдоевклидовой.

Пусть S – гладкая поверхность, - ее векторное уравнение и

Первой квадратичной формой поверхности S называют выражение I=.

Запишем это выражение подробнее. Имеем

откуда

. (25)

Выражение (25) в каждой точке поверхности S представляет собой квадратичную форму от дифференциалов du и dv.

Для коэффициентов первой квадратичной формы часто используют следующие обозначения:

.

Таким образом первая квадратичная форма имеет вид:

(26)

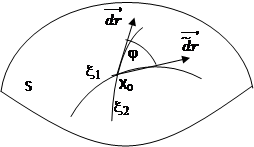
Угол между кривыми равен углу между касательными. Пусть гладкие кривые x1 и x2 лежат на поверхности S с векторным уравнением и пересекается в некоторой точке X0.

Вектор лежит в касательной плоскости к поверхности S в точке X0 (Рис.4.2).

Значения дифференциалов можно выбрать так, чтобы был вектором касательной к кривой x1 в точке X0. Достаточно взять () (здесь u=u(t) и v=v(t) – уравнения кривой x1 на поверхности S).

Аналогично строится вектор - вектор касательной к кривой x2 в точке X0, отвечающий значениям дифференциалов , функций, определяющих кривую x2:

.

Поэтому

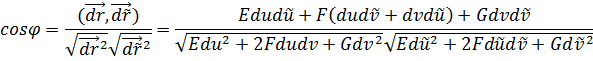
Требуется, чтобы ортогональные линии были ортогональны, т.е.

Учитывая, что u – естественный параметр, найдем коэффициенты E, F, G:

Подставляя полученные выражения в (26) имеем

Воспользовавшись (27) и полученными выражениями для коэффициентов, получим Разделим последнее равенство на , получим

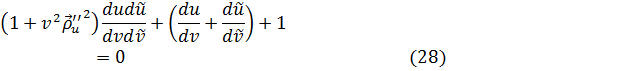
Исходное семейство линий задано дифференциальным уравнением

, а ортогональные траектории получены в виде Подставляя эти выражения в (28), имеем уравнение для , из которого . Учитывая, что исходное семейство линий – это v-линии, для которых du=0, а значит l=0, получим m=-1. Таким образом, , решая это дифференциальное уравнение, находим u+v=const – условие ортогональности траекторий. Итак, искомая замена координат имеет вид:

Тогда обратная замена:

Уравнение торса в новых координатах примет вид:

Обозначим U, V теми же символами u, v тогда уравнение торса перепишется следующим образом:

.(29)

Рассмотрим на торсе (29) кривую

u=u(t), v=v(t).(30)

Получим ее уравнение в виде:

. (31)

Направляющий вектор касательной:

. (32)

Касательная к любой кривой, лежащей на торсе и проходящей через данную точку N, лежит в плоскости Эта плоскость будет называться касательной плоскостью к торсу и обозначается

Найдем векторы . Из уравнения (29) получим:

.

 Скачать реферат