Дифференциальная геометрия торсов в пространстве 1R4 с псевдоевклидовой касательной плоскостью

(8)

Теорема 2.4. Для кривой g: , заданной в естественной параметризации, получим

(9)

Доказательство.

width=180 height=37 src="images/referats/11804/image149.png">.

Из (8) следует . Значит,и, следовательно,

, . (10)

Дифференцируем равенство (10): Отсюда,

Ч.т.д.

Вектор направлен по касательной в точке М: . Вектор выберем в соприкасающейся плоскости перпендикулярно :

Условие перпендикулярности к в соприкасающейся плоскости:Отсюда: .

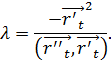
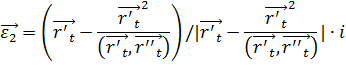
Вектор выберем в соприкасающейся 3-плоскости перпендикулярно векторам и .

(11)

Найти и можно используя условия ортогональности:

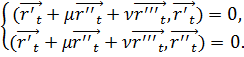
Подставив и в формулу (8) получим вектор .

Вектор выберем в 1R4 перпендикулярно ,,.

В нашем случае векторы ,,- векторы действительной длины, а вектор - вектор мнимой длины.

Пусть кривая g задана в естественной параметризации. Вектора ,, , канонического репера будут заданы тоже с помощью параметра s.

Рассмотрим векторы ,, . Эти векторы можно будет разложить по базису ,, :

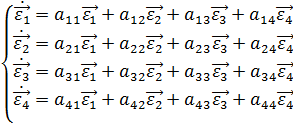(12)

Теорема 2.5. Производная вектора постоянной длины перпендикулярна этому вектору.

Доказательство.

Пусть

Ч.т.д.

Из теоремы 2.5. следует, что .

Домножим первое уравнение (12) скалярно на . Получим . Аналогично,

. (13)

Домножим первое уравнение (12) скалярно на , второе на , затем сложим их. (,)+(,)=+. Выражение =0.

Отсюда, = .

Аналогично, =, =, =, =,=.

Выберем , . При этом имеет действительную длину. Тогда

(14)

Исходя из (12) и (14), получим =. Следовательно, ==0.

 Скачать реферат