Предел последовательности. Теорема Штольца

Введение

Одним из основополагающих разделов курса математического анализа является раздел, изучающий теорию предела последовательности и предела функции. Данная теория является значимой для изучения многих других разделов математического анализа, а также других дисциплин математики.

Целью данной курсовой работы является доказательство теоремы Штольца. В работе подробно рассмотр

ены следующие аспекты: понятие предела последовательности, характерные примеры вычисления пределов последовательности с подробным разбором решения, теорема Штольца и примеры её применения.

Введение

Тема данной курсовой работы «Предел последовательности. Теорема Штольца». Для того чтобы углубиться в изучение данного вопроса, для начала, вспомним некоторые определения, утверждения и теоремы из начального изучения математического анализа, вплотную касающиеся основной проблемы затронутой в курсовой работе.

В физике и в других науках о природе встречалось множество различных величин: время, длина, объём, вес и т.п. Любая из них, смотря по обстоятельствам, то принимала различные значения, то лишь одно.

В математике, однако, мы отвлекаемся от физического смысла рассматриваемой величины, интересуясь лишь числом, которым она выражается физический смысл величины, снова приобретает важность, лишь, когда занимаются приложениями математики. Таким образом, для нас переменная величина (или короче – переменная) является отвлечённой или числовой переменной. Её обозначают каким-либо символом (буквой, например, х), которому приписывают числовые значения.

Переменная считается заданной, если указанно множество Х={х} Постоянную величину (короче – постоянную) удобно рассматривать как частный случай переменной; он отвечает предположению, что множество Х={х} состоит из одного элемента.

Перейдём к установлению понятия числовой последовательности.

Определение: если каждому nє N, поставлено в соответствие xnє N,то говорят, что

(1)

образуют числовую последовательность.

– члены последовательности

– общий член последовательности

Введённое определение подразумевает, что любая числовая последовательность должна быть бесконечна, но не означает, что все члены должны быть различные числа.

Числовая последовательность считается заданной, если указан закон, по которому можно найти любой член последовательности.

Члены или элементы последовательности (1) занумерованы всеми натуральными числами в порядке возрастания номеров. При n+1 > n-1 член следует за членом ( предшествует ), независимо от того, будет ли само число больше, меньше или даже равно числу .

Определение: Переменную x, принимающую некоторую последовательность (1) значений, мы – следуя Мерэ (Ch. Meray) – будем называть вариантой.

В школьном курсе математики можно встретить переменные именно такого типа, типа варианты.

Например, последовательность вида

(арифметическая) или вида

(геометрическая прогрессия)

Переменный член той или другой прогрессии есть варианта.

В связи с определением длины окружности обычно рассматривается периметр правильного вписанного в окружность многоугольника, получаемого из шестиугольника последовательным удвоением числа сторон. Таким образом, эта варианта принимает последовательность значений:

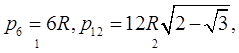
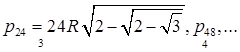
Упомянем ещё о десятичном приближении (по недостатку) к , со всё возрастающей точностью. Оно принимает последовательность значений:

и также представляет варианту.

Переменную x, пробегающую последовательность (1), часто обозначают через , отождествляя её с переменным («общим») членом этой последовательности.

Иногда варианта xпзадаётся тем, что указывает непосредственно выражение для xп; так, в случае арифметической или геометрической прогрессии имеем, соответственно, xп=а+(n-1) dили xп=aqn-1. Пользуясь этим выражением, можно сразу вычислять любое значение варианты по заданному его номеру, не вычисляя предыдущих значений.

Для периметра правильного вписанного многоугольника такое общее выражение возможно лишь, если ввести число π; вообще периметр рmправильного вписанного m-угольника даётся формулой

Предел последовательности

Определение 1: Числовая последовательность {хп} называется ограниченной сверху (снизу), если существует такое число М (т), что для любого элемента этой последовательности имеет место неравенство , при этом число М (т) называют верхней (нижней) гранью.

Определение 2: Числовая последовательность {хп} называется ограниченной, если она ограничена и сверху, и снизу, т.е. существуют М, т, что для любого

Обозначим А = max {|M|, |m|}, тогда очевидно, что числовая последовательность будет ограничена, если для любого выполняется равенство |xn|≤А, последнее неравенство есть условие ограниченности числовой последовательности.

Определение 3: числовая последовательность называется бесконечно большой последовательностью, если для любого А>0, можно указать такой номер N, что для всех n>N выполняется ||>A.

Определение 4: числовая последовательность {αn} называется бесконечно малой последовательностью, если для любого наперёд заданного ε > 0, можно указать такой номер N(ε), что для любого n > N(ε) будет выполняться неравенство | αn | < ε.

 Скачать реферат