Методы компьютерных вычислений и их приложение к физическим задачам

Mathematica.

Разрабатывается фирмой Wolfram Research. Одна из наиболее сложных для освоения систем. Предназначена в основном для решения теоретических задач, в связи с чем весьма популярна в научных кругах. Предуставляет широкие возможности в проведении символических (аналитических) преобразований, красотой интерфейса не отличается.

Maple.

Разработка компании Waterloo

Maple Inc. Также очень популярный в научных кругах пакет аналитических преобразований и численных методов. Символический процессор Maple поставляется отдельно, в связи с чем производители других программных средств могут интегрировать его в свои разработки.

4. Численное интегрирование

Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином)

. То есть:

,

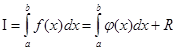где 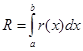– априорная погрешность метода на интервале интегрирования,

а r(x) – априорная погрешность метода на отдельном шаге интегрирования.

Обзор методов интегрирования.

Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными).

1) Методы Ньютона-Котеса. Здесь φ(x) – полином различных степеней. Сюда относятся метод прямоугольников, трапеций, Симпсона.

2) Методы статистических испытаний (методы Монте-Карло). Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов.

3) Сплайновые методы. Здесь φ(x) – кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов.

4) Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор весовых коэффициентов ρ(x) в задаче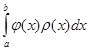. Сюда относится метод Гаусса-Кристоффеля (вычисление несобственных интегралов) и метод Маркова.

Метод прямоугольников.

Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.

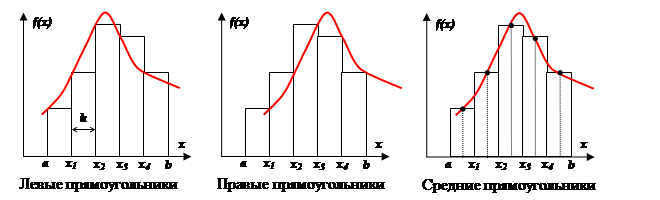
Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = xi.

…

Рассмотрим диапазон интегрирования от xi до xi + h, где h – шаг интегрирования.

Вычислим

…=

==.

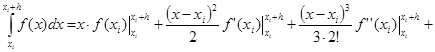Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.

В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид

.

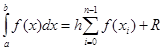Здесь n – число разбиений интервала интегрирования,

.

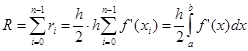Для справедливости существования этой оценки необходимо существование непрерывной f’(x).

Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке

,

то есть

.

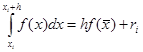Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

.

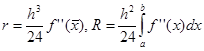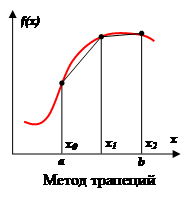
Метод трапеций.

Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка.

На единичном интервале.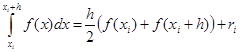

В случае равномерной сетки (h = const)

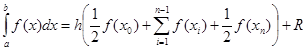
При этом , а 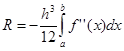. Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Особенности поведения погрешности.

Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину шага интегрирования.

Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимости от числа n разбиений интервала (то есть при шаг ). На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя Rmin, которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R.

Уточняющая формула Ромберга.

Метод Ромберга заключается в последовательном уточнении значения интеграла при кратном увеличении числа разбиений. В качестве базовой может быть взята формула трапеций с равномерным шагом h.

Обозначим интеграл с числом разбиений n = 1 как

.

Уменьшив шаг в два раза, получим

.

Если последовательно уменьшать шаг в 2n раз, получим рекуррентное соотношение для расчета

.

Пусть мы вычислили четыре раза интеграл с n от 1 до 4. Представим следующий треугольник:

R(1;1)

R(2;1) R(2;2)

R(3;1) R(3;2) R(3;3)

R(4;1) R(4;2) R(4;3) R(4;4)

В первом столбце стоят значения интеграла, полученные при последовательном удвоении числа интервалов. Следующие столбцы – результаты уточнения значения интеграла по следующей рекуррентной формуле:

 Скачать реферат