Методы компьютерных вычислений и их приложение к физическим задачам

,

где i = 1…p, p – число уравнений в системе.

;

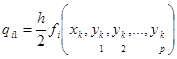k – номер точки, для которой осуществляется расчет;

;

;

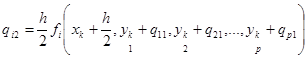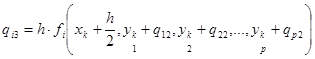h=307 height=59 src="images/referats/7507/image274.png">.

К достоинствам метода следует отнести высокую точность вычислений. Схемы более высокого порядка точности практически не употребляются в силу своей громоздкости. Также немаловажно, что метод является явным, т.е. значение yk+1 вычисляется по ранее найденным значениям за известное заранее число действий.

Все представленные выше схемы допускают расчет с переменным шагом. Например, шаг можно уменьшить там, где функция быстро изменяется, и увеличить в обратном случае. Так, метод Рунге-Кутты-Мерсона позволяет оценивать погрешность на каждом шаге и, в зависимости от полученной оценки принимать решение об изменении шага. Автоматический выбор шага позволяет значительно сократить время вычислений.

Метод Рунге – Кутта - Мерсона.

Этот метод отличается от метода Рунге – Кутта четвертого порядка возможностью оценивать погрешность на каждом шаге и в зависимости от этого принимать решение об изменении шага. Один из вариантов формул:

;

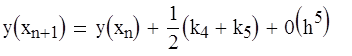
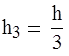
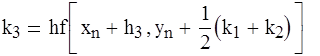
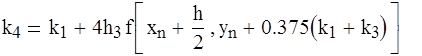
Rn+1 = 0.2k4 – 0.3k3 – 0.1k5 - погрешность на каждом шаге.

Пусть задана максимальна погрешность . Если , h = h/2 , и n+1 цикл расчета повторяется (с точки xn, yn) c новым шагом. Если же

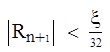, h = 2h

Автоматический выбор шага позволяет значительно сократить время решения ОДУ.

Схема РКМ обобщается на системы ОДУ аналогично классической схеме Рунге – Кутта.

Метод Адамса.

Метод основан на аппроксимации интерполяционными полиномами правых частей ОДУ.

Пусть с помощью любого из методов, рассмотренных выше, вычислено решение заданного дифференциального уравнения в точках x1, x2, x3 (а в точке x0 решение и так известно – поставлена задача Коши). Полученные значения функции обозначим как y0, y1, y2, y3, а значения правой части дифференциального уравнения как f0, f1, f2, f3, где fk = f(xk, yk). Начиная с четвертой точки, на каждом шаге интегрирования дифференциального уравнения вычисления осуществляются по схеме

P(EC){m}E

где P – прогноз решения; Е – вычисление f(x,y); С – коррекция решения; m – количество итераций коррекции. Схемы такого типа называют «прогноз-коррекция»: это подразумевает сначала приблизительное вычисление решение по формуле низкого порядка, а затем уточнение с учетом полученной информации о поведении интегральной кривой.

Прогноз осуществляется по экстраполяционной формуле Адамса:

. (10)

Коррекция осуществляется по интерполяционной формуле Адамса:

. (11)

Вычисление осуществляется по формуле:

Количество итераций m ≤ p, где p – порядок используемого метода. В ходе каждой итерации решается нелинейное уравнение (11) относительно неизвестной y4 (обычно методом простых итераций).

Иногда в методе Адамса используется схеме PECE на каждом шаге процесса интегрирования, т.е. осуществляется только одна коррекция. В силу сложности вычислений метод используется только в мощных программных пакетах численного анализа. Формулы метода также легко переносятся на решение систем ОДУ первого порядка.

Постановка краевой задачи. Метод стрельбы.

Краевая задача – задача отыскания частного решения системы

(12),

1 ≤ k ≤ p, на отрезке a ≤ x ≤ b, на котором дополнительные условия налагаются на значения функции uk(x) более чем в одной точке этого отрезка. В качестве примера моно привести задачу нахождения статического прогиба u(x) нагруженной струны с закрепленными концами:

, a ≤ x ≤ b, u(a) = u(b) = 0.

Здесь f(x) имеет смысл внешней изгибающей нагрузки на единицу длины струны, деленной на упругость струны.

Найти точное решение краевой задачи в элементарных функциях удается редко: для этого надо найти общее решение системы (12) и суметь явно определить из краевых условий значения входящих в него постоянных. Одним из методов, предполагающих численное решение поставленной задачи, является метод стрельбы, в котором краевая задача для системы (12) сводится к задаче Коши для той же системы.

Рассмотрим систему двух дифференциальных уравнений первого порядка

(13)

с краевыми условиями

(14)

Сначала выберем некоторое значение , так что . Это уравнение мы можем решить и определить . Таким образом у нас появились два числа и β, которые будут определять задачу Коши , для системы (13), удовлетворять левому краевому условию, но не удовлетворять второму уравнению (14). Тем не менее, решим систему ОДУ с задачей Коши каким-либо из известных нам численных методов. Получим решение вида

(15), зависящее от как от параметра.

Теперь мы должны каким-либо способом менять параметр до тех пор, пока не подберется такое значение, для которого будет выполнено условие (16), т.е. правое краевое условие. Для этого случайным образом берут значения до тех пор, пока среди величин не окажется разных по знаку.

 Скачать реферат