Методы компьютерных вычислений и их приложение к физическим задачам

Метод градиентного (наискорейшего) спуска.

В этом методе функция минимизируется по направлению, в котором она быстрее всего убывает, т.е. в направлении, обратном .

Вдоль этого направления функция зависит от одной параметрической перемен

ной t, для нахождения минимума которой можно воспользоваться любым известным методом поиска минимума функции одной переменной. Спуск из точки начального приближения против градиента до минимума t определяет новую точку , в которой вновь определяется градиент и делается следующий спуск. Условием окончания процесса, как и в случае координатного спуска, будет .

С помощью метода градиентного спуска минимум гладких функций в общем случае находится быстрее, чем при использовании координатного спуска, однако нахождение градиента численными методами может свести на нет полученный выигрыш. Сходимость плохая для функций с овражным рельефом, т.е. с точки зрения сходимости градиентный спуск не лучше спуска по координатам.

Каждый спуск заканчивается в точке, где линия градиента касательна к линии (поверхности) уровня. Это означает, что каждый следующий спуск должен быть перпендикулярен предыдущему. Таким образом, вместо поиска градиента в каждой новой точке можно сосчитать градиент в начальной точке, и развернуть оси координат так, чтобы одна их осей была параллельна градиенту, а затем осуществлять спуск координатным методом.

Метод оврагов.

Ставится задача найти минимум для овражной функции.

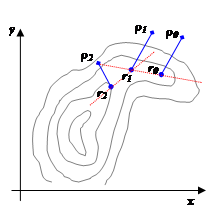
Для этого выбираются две близкие точки и , и осуществляется спуск из этих точек (любым методом), причем высокой точности сходимости не требуется. Конечные точки спуска и будут лежать вблизи дна оврага. Затем осуществляется движение вдоль прямой, соединяющей и в сторону уменьшения (как бы вблизи дна оврага). Движение может быть осуществлено только на один шаг ~ h, направление выбирается из сравнения значения функции в точках и . Таким образом, находится новая точка . Так как возможно, что точка уже лежит на склоне оврага, а не на дне, то из нее снова осуществляется спуск в новую точку . Затем намечается новый путь по дну оврага вдоль прямой, соединяющей и . Если – процесс прекращается, а в качестве минимума в данном овраге используется значение .

Метод оврагов рассчитан на то, чтобы пройти вдоль оврага и выйти в котловину около минимума. В этой котловине значения минимума лучше уточнять другими методами.

Проблемы поиска минимума в задачах с большим числом измерений.

Пусть в n-мерном векторном пространстве задана скалярная функция . Наложим дополнительные условия , 1 ≤ i ≤ m; , 1 ≤ j ≤ p. Условия типа равенств выделяют в пространстве некоторую (n – m)-мерную поверхность, а условия типа неравенств выделяют n-мерную область, ограниченную гиперповерхностями . Число таких условий может быть произвольным. Следовательно, задача infесть поиск минимума функции n переменных в некоторой (n – m)-мерной области E. Функция может достигать минимального значения как внутри области, так и на ее границе. Однако перейти к (n – m)-мерной системе координат практически никогда не удается, поэтому спуск приходится вести во всем n-мерном пространстве.

Даже если нулевое приближение лежит в области E, естественная траектория спуска сразу выходит из этой области. Для принудительного возврата процесса в область E, например, используется метод штрафных функций: к прибавляются члены, равные нулю в E, и возрастающие при нарушении дополнительных условий (ограничений). Метод прост и универсален, однако считается недостаточно надежным. Более качественный результат дает использование симплекс-методов линейного программирования, однако данный вопрос в рамках настоящего курса не рассматривается.

13. Решение обыкновенных дифференциальных уравнений.

Постановка задачи. Типы задач для ОДУ.

Известно, что с помощью дифференциальных уравнений можно описать задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, и др. Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка, или к системе уравнений любого порядка. Так как любое ОДУ порядка p

u(p)(x) = f(x, u, u/, u//, … u(p+1)) заменой u(k)(x) = yk(x) можно свести к эквивалентной системе из p уравнений первого порядка, представленных в каноническом виде :

y/k(x) = yk+1(x) для 0 ≤ k ≤ p–2 (1)

y/p-1(x) = f(x, y0, y1, … yp–1), при этом y0(x) ≡ u(x). (2)

Покажем такое преобразование на примере уравнения Бесселя:

.

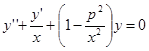Предполагая тождественную замену y1(x) ≡ y(x) представим систему ОДУ в следующем виде:

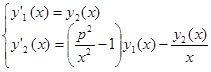
Аналогично произвольную систему дифференциальных уравнений любого порядка можно заменить некоторой эквивалентной системой уравнений первого порядка. Следовательно, алгоритмы численного решения достаточно реализовать для решения системы дифференциальных уравнений первого порядка.

Известно, что система p-го порядка имеет множество решений, которые в общем случае зависят от p параметров {C1, C2, … Cp}. Для определения значений этих параметров, т.е. для выделения единственного решения необходимо наложить p дополнительных условий на uk(x). По способу задания условий различают три вида задач, для которых доказано существование и единственность решения. Это

 Скачать реферат