Методы компьютерных вычислений и их приложение к физическим задачам

Если это осуществилось, пара таких значений определяет интервал , который можно обработать методом дихотомии до получения корня уравнения (16). Нахождение каждого нового значения функции (16) требует нового численного интегрирования для решения ОДУ, что делает этот метод достаточно медленным.

Решение уравнений в частных прои

зводных.

К уравнениям в частных производных приводят задачи газодинамики, теплопроводности, переноса излучения, электромагнитных полей, процессов переноса в газах, и др. Независимыми переменными в физических задачах обычно являются время t, координаты , скорости частиц . Пример – уравнение теплопроводности

, (17)

где U – температура, – теплоемкость, – коэффициент теплопроводности, q – плотность источников тепла.

Для решения дифференциальных уравнений в частных производных применяется сеточный метод, суть которого – в разбиении области, в которой ищется решение, сеткой узлов заданной конфигурации, после чего составляется разностная схема уравнения и находится его решение, например методом разностной аппроксимации.

Рассмотрим в качестве примера одномерную задачу, близкую по смыслу к (17):

. (18)

Здесь 0 ≤ x ≤ a, 0 ≤ t ≤ T.

Граничные условия:

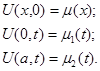
Для одной и той же задачи можно составить много разностных схем. Метод разностной аппроксимации заключается в том, что каждая производная, входящая в дифференциальное уравнение и краевые условия, заменяется разностным выражением, включающим в себя только значения в узлах сетки.

Введем равномерную прямоугольную сетку по x и t с шагом h и τ соответственно и заменить производные соответствующими разностными отношениями. Тогда

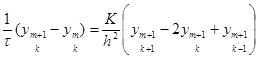. (19)

Здесь 1 ≤ k ≤ N-1 – число точек по координате x; 0 ≤ m ≤ M – число точек по координате t. Число неизвестных в (19) больше числа уравнений, недостающие уравнения выводятся из начальных и граничных условий:

; 0 ≤ k ≤ N.

; ; 0 ≤ m ≤ M.

Схема (19) содержит в каждом уравнении несколько неизвестных значений функции. Такие схемы называют неявными. Для фактического вычисления решения следует переписать схему так:

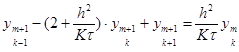, где 1 ≤ k ≤ N-1.

; . (20)

Теперь схема представляет собой систему линейных уравнений для определения величин ; правые части этих уравнений известны, поскольку содержат значения решений для предыдущего индекса времени.

Другим вариантом решения сеточной задачи является использование интегро-интерполяционных методов (методов баланса), в которых дифференциальное уравнение интегрируют по ячейке сетки, приближенно вычисляя интегралы по квадратурным формулам.

Приложение 1.

Случайные величины в компьютерном моделировании.

Параметры случайных величин.

Величину ξ называют случайной с плотностью распределения ρ(x), если вероятность того, что величина примет значения между x1 и x2, равна

.

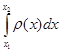Псевдослучайные распределения. Иллюстрация возможностей Mathcad.

Моделирование броуновского движения в системе MathLab.

Литература

1. Н. Бахвалов, Н. Жидков, Г. Кобельков. Численные методы. М., 2002, 632 с.

2. Н. Калиткин. Численные методы. М., 1972,

3. А. Мудров. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск, 1992, 270с.

4. А. Самарский. Введение в численные методы. М., , 270с.

5. Ю. Тарасевич. Численные методы на Mathcad’е. Астрахань, 2000, 70с.

6. Г. Коткин, В. Черкасский. Компьютерное моделирование физических процессов с использованием MathLab. Новосибирск, 2001.

7. М. Лапчик, М. Рагулина, Е. Хеннер. Численные методы.М., 2004, 384с.

 Скачать реферат